数据结构
绪论
基本概念和术语
数据: 所有能输入到计算机中并被计算机程序处理的符号的总称. (图像,
声音等都算)
数据元素: 数据的基本单位.
有时候一个数据元素可以由若干个数据项组成.
数据项: 数据的不可分割的最小单位.
数据对象: 性质相同的数据元素的集合. 是数据的一个子集.
数据结构: 相互之间存在一种或多种特定关系的数据元素的集合.
数据元素相互之间的关系称为"结构".
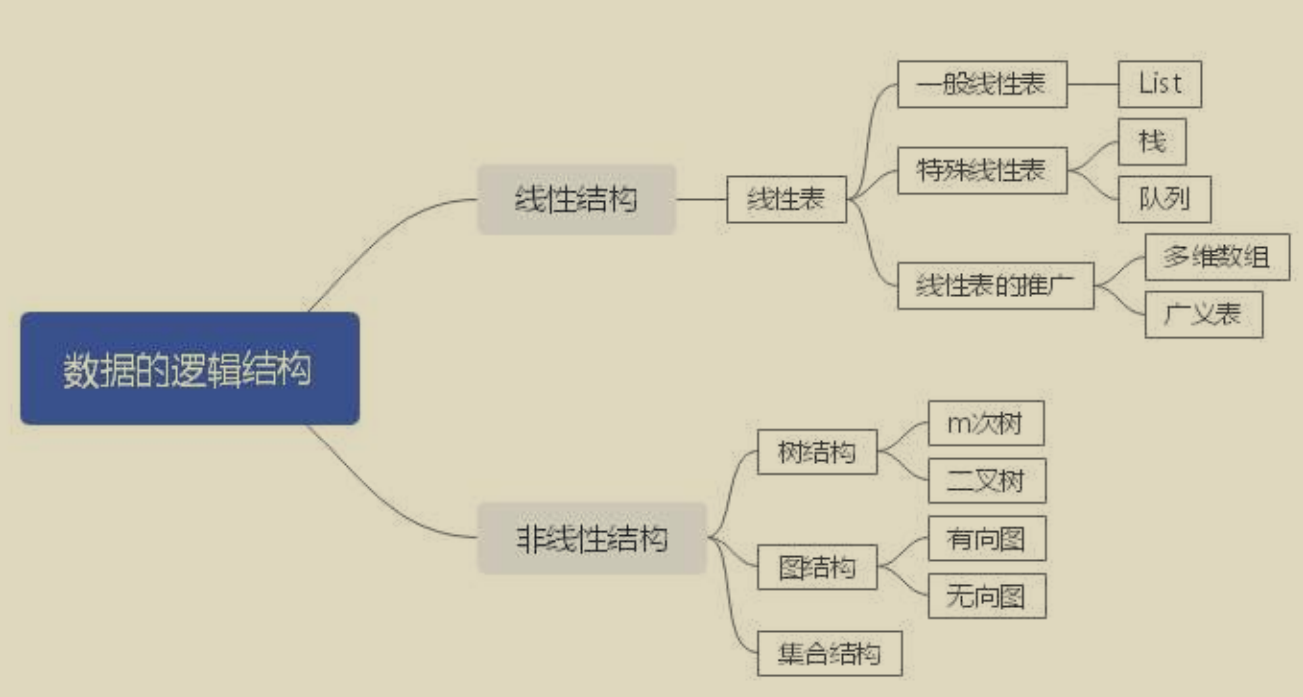
数据结构包括逻辑结构和存储结构两个层次.
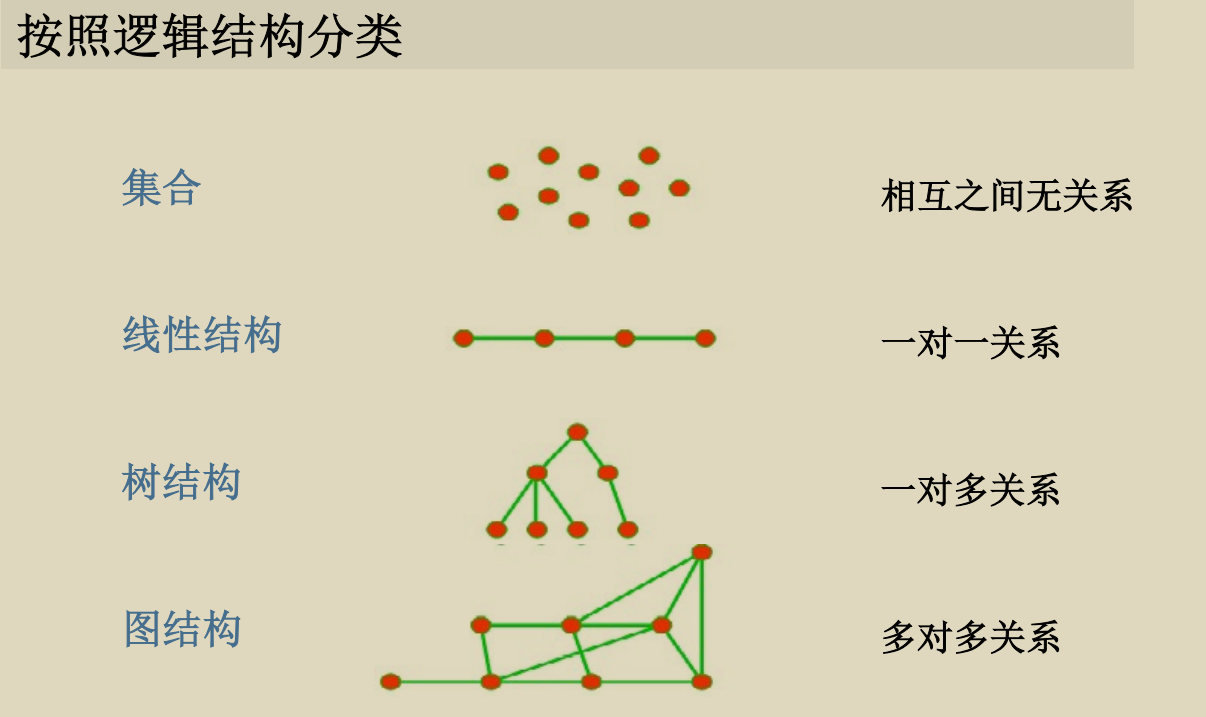
逻辑结构: 描述的是数据元素之间的逻辑关系. 主要有: 集合, 线性结构,
树结构, 图结构.
存储结构: 数据结构再计算机中的存储称为数据的存储结构, 也称为物理结构.
主要有: 顺序存储结构和链式存储结构.
数据类型:
数据类型是一个值的集合和定义在这个值集上的一组操作的总称.
抽象数据类型( ADT ) : 一般指由用户定义的, 表示应用问题的数学模型,
以及定义在这个模型上的一组操作的总称. 具体包括三个部分:
数据对象, 数据对象上的关系的集合, 数据对象的基本操作的集合.
算法和算法分析
上述式子从左往右数量级递增.
主要考虑执行次数最多的语句, 显然是第二个 for 或者 sum. 总的执行次数是
1 + 2 + 4 + ... + 2k . 并且 2k < n. 求和为
2k - 1 近似于 2n - 1. 因此选 B.
线性表
本章内容
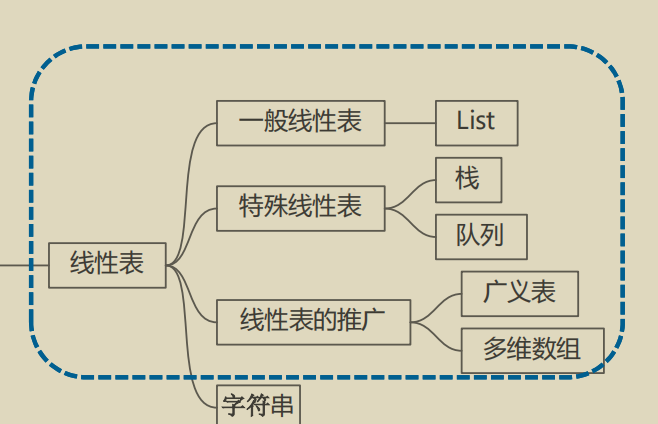
线性表的定义和特点
线性表的类型定义
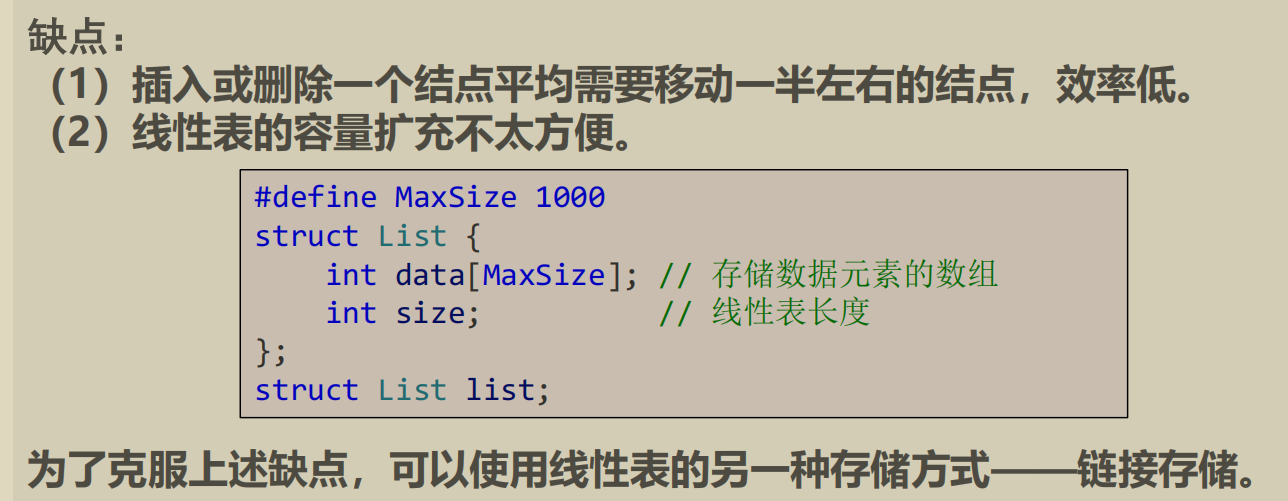
顺序存储的线性表
顺序存储线性表( List
)的类的定义和部分实现
#define NIL -1 typedef int Position; template <typename ElemType>class List {private :ElemType *data_; Position last_; Position maxsize_; public :struct ListException { std::string error_; ListException (std::string s):error_ (s){};}; List (unsigned =kMaxSize); List (const List&); List& operator =(const List&); ~List (); Position Search (ElemType x) ; void Insert (Position i,ElemType x) void Remove (Position i) template <typename U>friend std::ostream& operator <<(std::ostream&, const List<U>&); template <typename U>friend std::istream& operator >>(std::istream&, List<U>&); };
这个代码写的还可以. 可以学一下异常处理和输入输出函数的定义.
另外就是模板的使用.
template <typename ElemType>List<ElemType>::List (unsigned list_size) { data_ = new ElemType[list_size]{0 }; last_ = NIL; maxsize_ = list_size; } template <typename ElemType>List<ElemType>::List (const List& li) { data_ = new ElemType[li.maxsize_]{0 }; maxsize_ = li.maxsize_; last_ = li.last_; for (int i=0 ; i<=last_ ;i++) { data_[i] = li.data_[i]; } } template <typename ElemType>List<ElemType>& List<ElemType>::operator =(const List& li) { if (this != &li) { delete [] data_; data_ = new ElemType[li.maxsize_]{0 }; maxsize_ = li.maxsize_; last_ = li.last_; for (int i=0 ; i<=last_ ;i++) { data_[i] = li.data_[i]; } } return *this ; } template <typename ElemType>List<ElemType>::~List () { delete [] data_; last_ = NIL; } template <typename ElemType>std::ostream& operator <<(std::ostream& os, const List<ElemType>& llist) { for (int i=0 ; i<=llist.last_ ;i++){ os << llist.data_[i] << ' ' ; } return os; }
下面的 cin 部分比较有意思:
template <typename ElemType>std::istream& operator >>(std::istream& is, List<ElemType>& llist) { int n; is >> n; if ( n > (llist.maxsize_)) { throw List<ElemType>::ListException ("元素个数超过线性表最大容量。\n" ); } llist.last_ = n-1 ; for (int i = 0 ; i < n; i++) { is >> llist.data_ [i] ; } return is; } int main () List<int > mylist; try { std::cin >> mylist; std::cout << mylist << std::endl; } catch (List<int >::ListException e) { std::cout << e.error_; std::cout << mylist << std::endl; } return 0 ; }
首先, throw 后面跟着的必须是一个对象.
我们为先前在类中定义好的异常结构体传入对应的字符串进行初始化,
作为throw的对象.
为了顺利抛出异常, 需要使用 try 和 catch 语句. 在 try 中触发了 throw,
那么 throw 后面跟着创建的临时变量就会被 catch 获取. 在 catch
的括号中我们给这个临时变量命名为 e. 然后使用 e 中我们定义好的变量 error
作为输出
之前学了异常处理一直不知道咋用, 现在终于遇到应用场景了.
顺序存储线性表的插入和删除
void Insert (List* list, int i, int x) int j; if (list->size == MaxSize) { printf ("错误:表满不能插入。\n" ); return ; } if ((i < 0 ) || (i > list->size)) { printf ("错误:插入位置不合法。\n" ); return ; } for (j = list->size; j > i; j--) { list->data[j] = list->data[j - 1 ]; } list->data[i] = x; list->size++; }
void Remove (List* list, int i) int j; if ((i < 0 ) || i >= list->size) { printf ("错误:不存在这个元素。\n" ); return ; } for (j = i + 1 ; j < list->size; j++) { list->data[j - 1 ] = list->data[j]; } list->size--; }
顺序存储线性表的应用
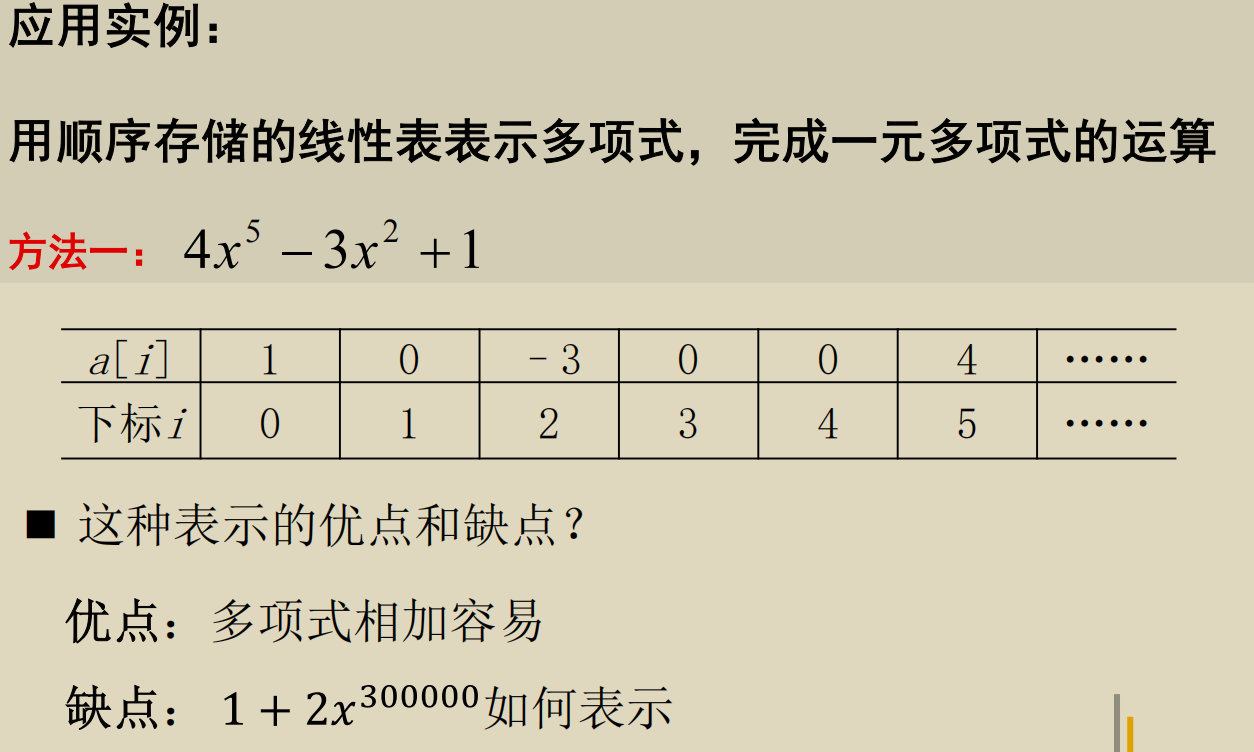
多项式的表示
第二种是要更好的.
多项式相加
Poly polyADD (Poly p1, Poly p2) Poly result; int i = 0 , j = 0 , k = 0 ; double sum = 0 ; while (i < p1. size && j < p2. size) { if (p1. data[i].exp > p2. data[j].exp) { result.data[k++] = p1. data[i++]; } else if (p1. data[i].exp < p2. data[j].exp) { result.data[k++] = p2. data[j++]; } else { sum = p1. data[i].coef + p2. data[j].coef; if (sum > eps || sum < -eps) { result.data[k].coef = sum; result.data[k].exp = p1. data[i].exp; k++; } i++; j++; } } while (i < p1. size) { result.data[k++] = p1. data[i++]; } while (j < p2. size) { result.data[k++] = p2. data[j++]; } result.size = k; return result; }
这里注意一下 eps 代表 epsilon. 意思是一个极小的数. 这是因为两个
double 相加可能是 0, 但是由于精度限制它们实际上很难等于0, 所以要使用 eps
来近似0, 而不能是 sum == 0.
总结
链式存储的线性表
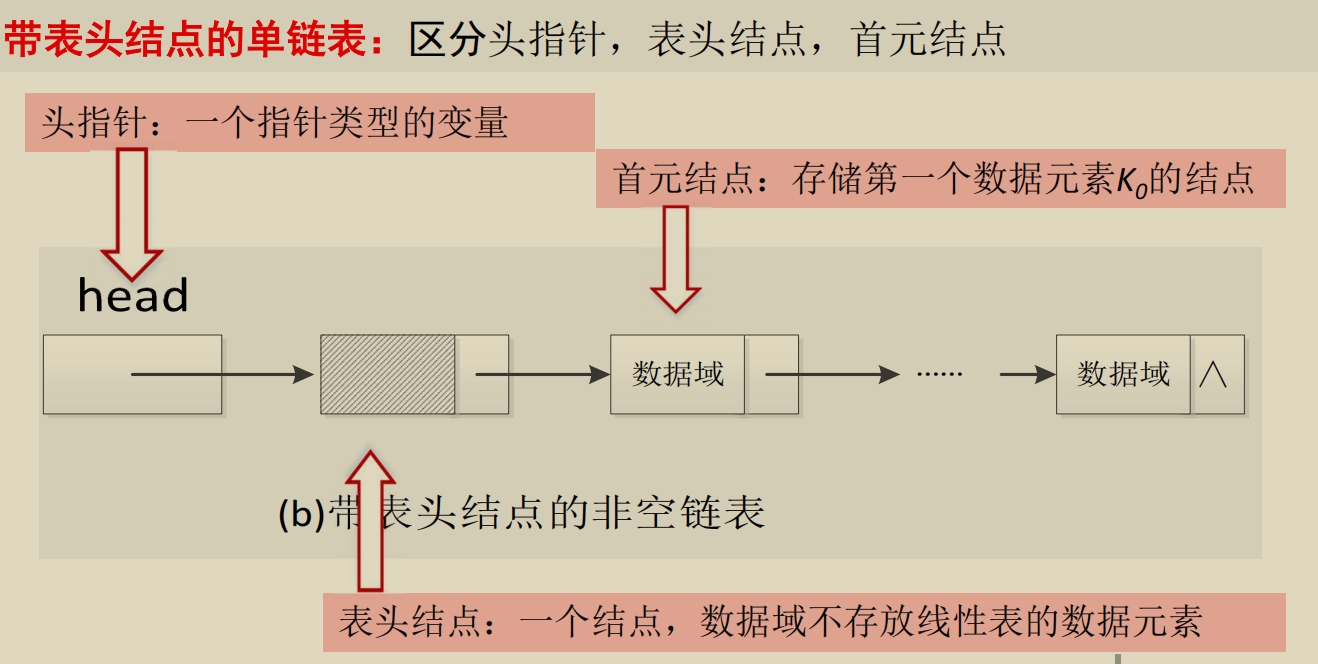
单链表的定义和表示
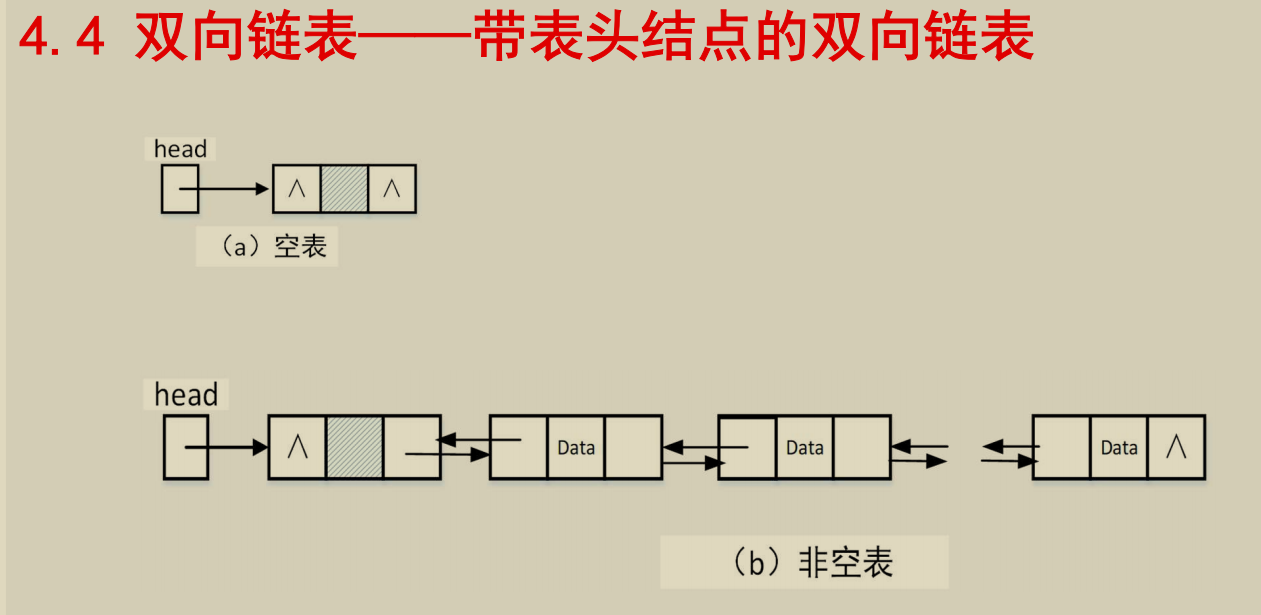
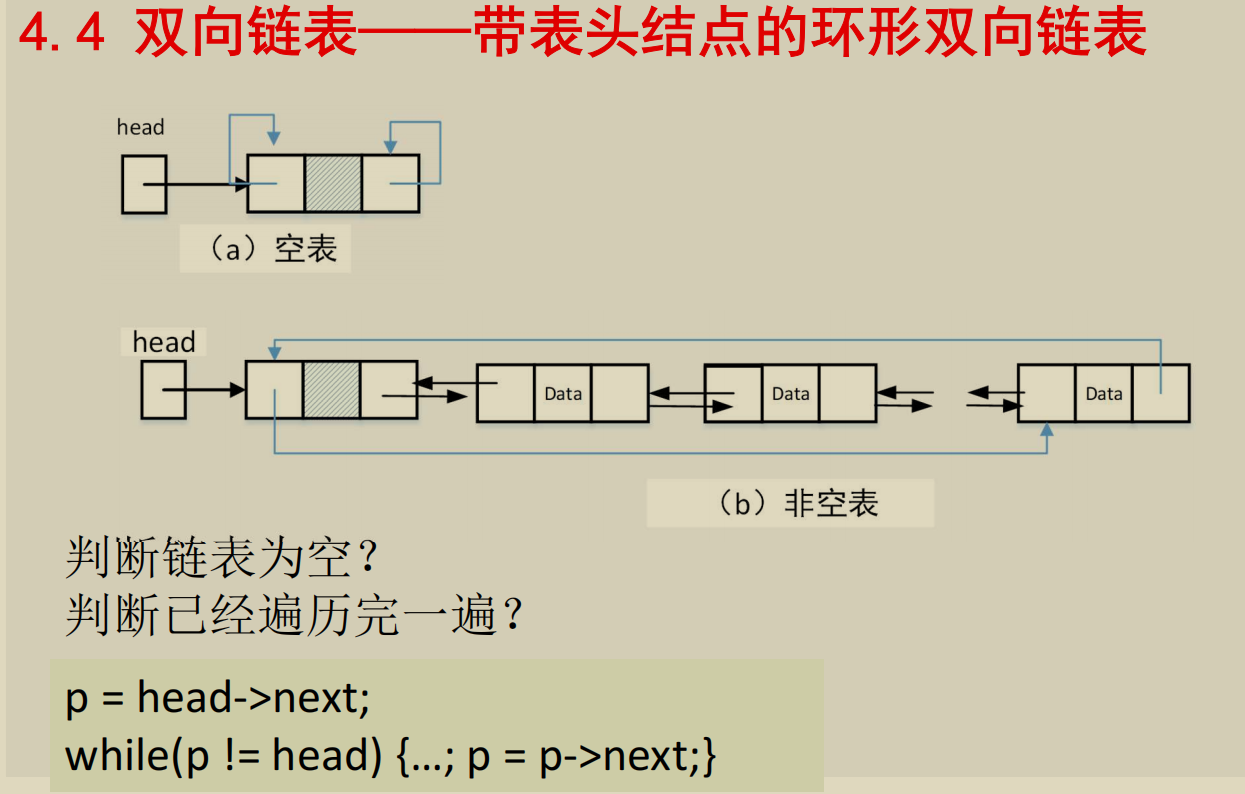
注意区分表头节点和首元节点. 在前者存在时, 头指针指向前者,
在前者不存在时, 头指针指向后者.
单链表基本操作的实现
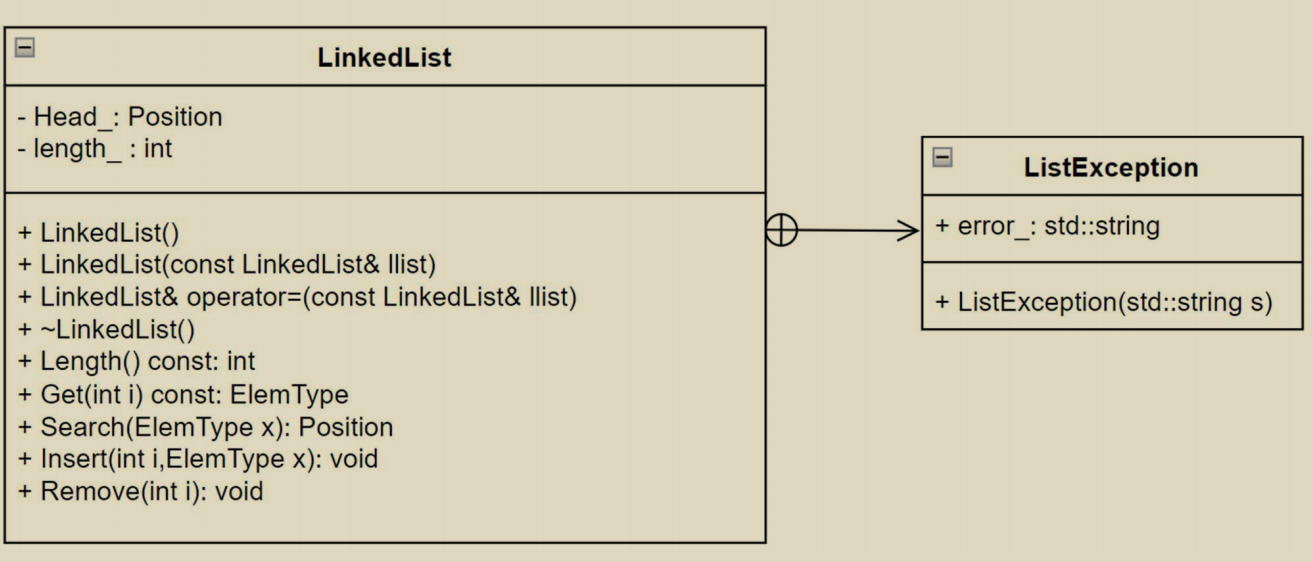
类定义和实现
#define NIL nullptr template <typename ElemType>class LinkedList { public : struct ListNode { ElemType data_; ListNode* next_; }; using Position = ListNode*; struct ListException { std::string error_; ListException (std::string s) : error_ (s) {}; }; LinkedList (); LinkedList (const LinkedList&); LinkedList& operator =(const LinkedList&); ~LinkedList (); int Length () const ElemType Get (int i) const ; Position Search (ElemType x) ; void Insert (int i, ElemType x) void Remove (int i) private : Position head_; int length_; };
这里用 Position 指代指针, 或者说地址.
构造函数:
template <typename ElemType>LinkedList<ElemType>::LinkedList () { head_ = NIL; length_ = 0 ; } template <typename ElemType>LinkedList<ElemType>::LinkedList (const LinkedList& llist) { Position temp, p; temp = llist.head_; length_ = llist.length_; head_ = new ListNode{ 0 , NIL }; p = head_; while (temp != NIL) { p->next_ = new ListNode{ temp->data_, NIL }; p = p->next_; temp = temp->next_; } p = head_; head_ = head_->next_; delete p; }
copy 这一部分还是需要细看的. 可以问自己几个问题:
一个单链表有什么东西? 回看一下我们定义的变量就知道了.
明确了以后, 每个变量应该等于什么呢? 显然 length 应该相同. 而 head
肯定要重新搞一个地址. 这里我们进行的操作是创建一个临时的空节点,
再用一个临时指针 p 通过不断地 next 完成对另一个链表的赋值, 最后让 head
指向首元节点. (head_ = head_->next_;). 关键的理解点就是:
在 head
指向了一个临时节点后(head_ = new ListNode{ 0, NIL };), head
的 next 指向就是首元节点. 而我们最后需要的是
head本身指向首元节点.
那其实说到这里已经初见端倪. 也即: 这里的代码是不使用 "表头节点"
的. 进一步思考, 如果使用了表头节点, 那么就不需要
p = head_; head_ = head_->next_; delete p;
这几行代码了. 前面那样就能够符合表头节点存在时链表的形式了.
template <typename ElemType>LinkedList<ElemType>& LinkedList<ElemType>::operator =(const LinkedList& llist) { Position p, temp; if (this != &llist) { p = head_; while (p != NIL) { head_ = p->next_; delete p; p = head_; } length_ = 0 ; temp = llist.head_; length_ = llist.length_; head_ = p = new ListNode{ 0 , NIL }; while (temp != NIL) { p->next_ = new ListNode{ temp->data_, NIL }; p = p->next_; temp = temp->next_; } p = head_; head_ = head_->next_; delete p; } return *this ; }
几乎相同的原理. 不过这里加了个 if 语句块将当前链表置为初始状态.
析构函数:
template <typename ElemType>LinkedList<ElemType>::~LinkedList () { Position p = head_; while (p != NIL) { head_ = p->next_; delete p; p = head_; } length_ = 0 ; }
为了防止内存泄漏, 需要一个个删掉.
单链表基本操作实现
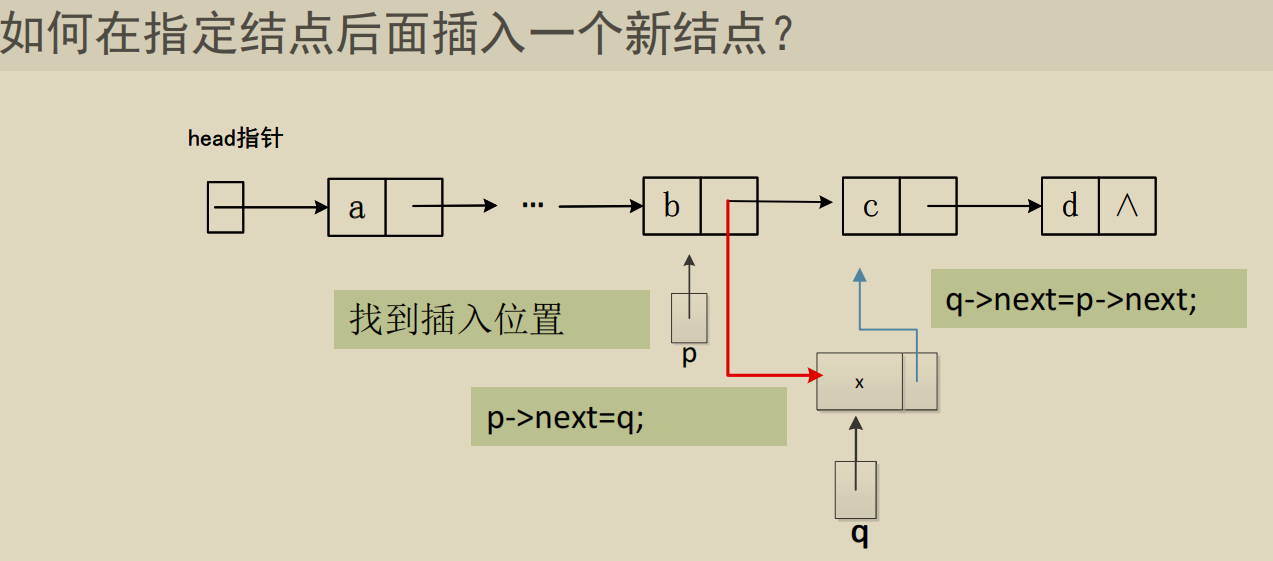
插入:
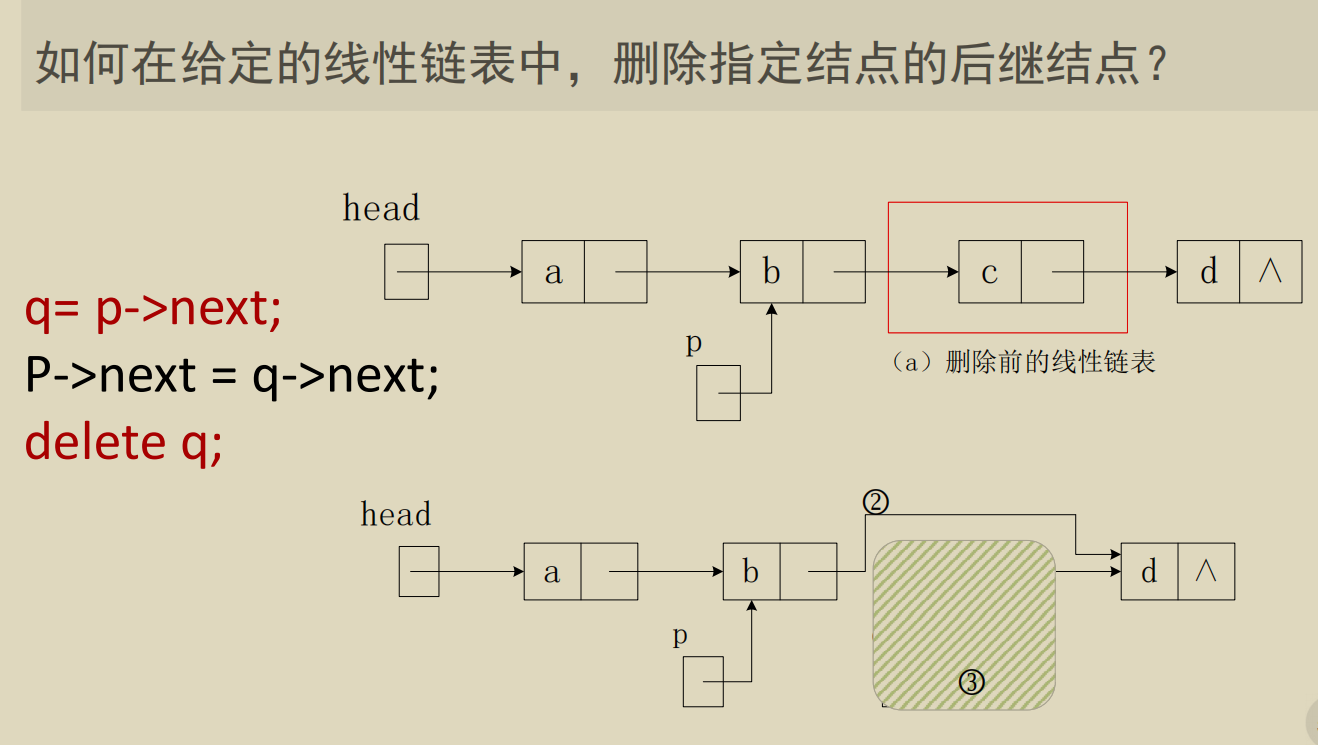
删除:
用线性链表表示多项式
#include <cmath> #include <iostream> #include <iomanip> typedef double CoefType; #define NIL nullptr #define eps (1e-9) typedef struct PolyNode * Position; struct PolyNode { CoefType coef_; int expon_; Position next_; }; class Polynomial { private : Position head_; Position rear_; public : struct PolyException { std::string error_; PolyException (std::string s) : error_ (s) {}; }; Polynomial (); Polynomial (const Polynomial&); Polynomial& operator =(const Polynomial&); ~Polynomial (); void Attach (CoefType, int ) friend Polynomial PolynomialAdd (const Polynomial&, const Polynomial&) friend std::ostream& operator <<(std::ostream&, const Polynomial&); friend std::istream& operator >>(std::istream&, Polynomial&); };
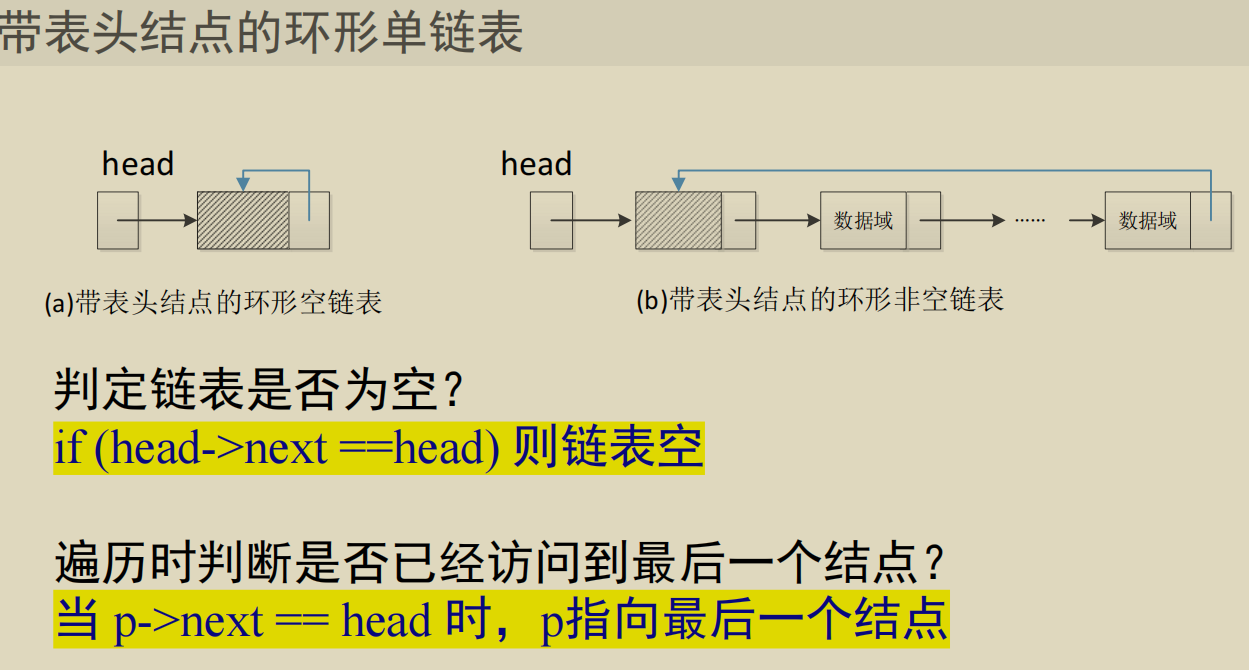
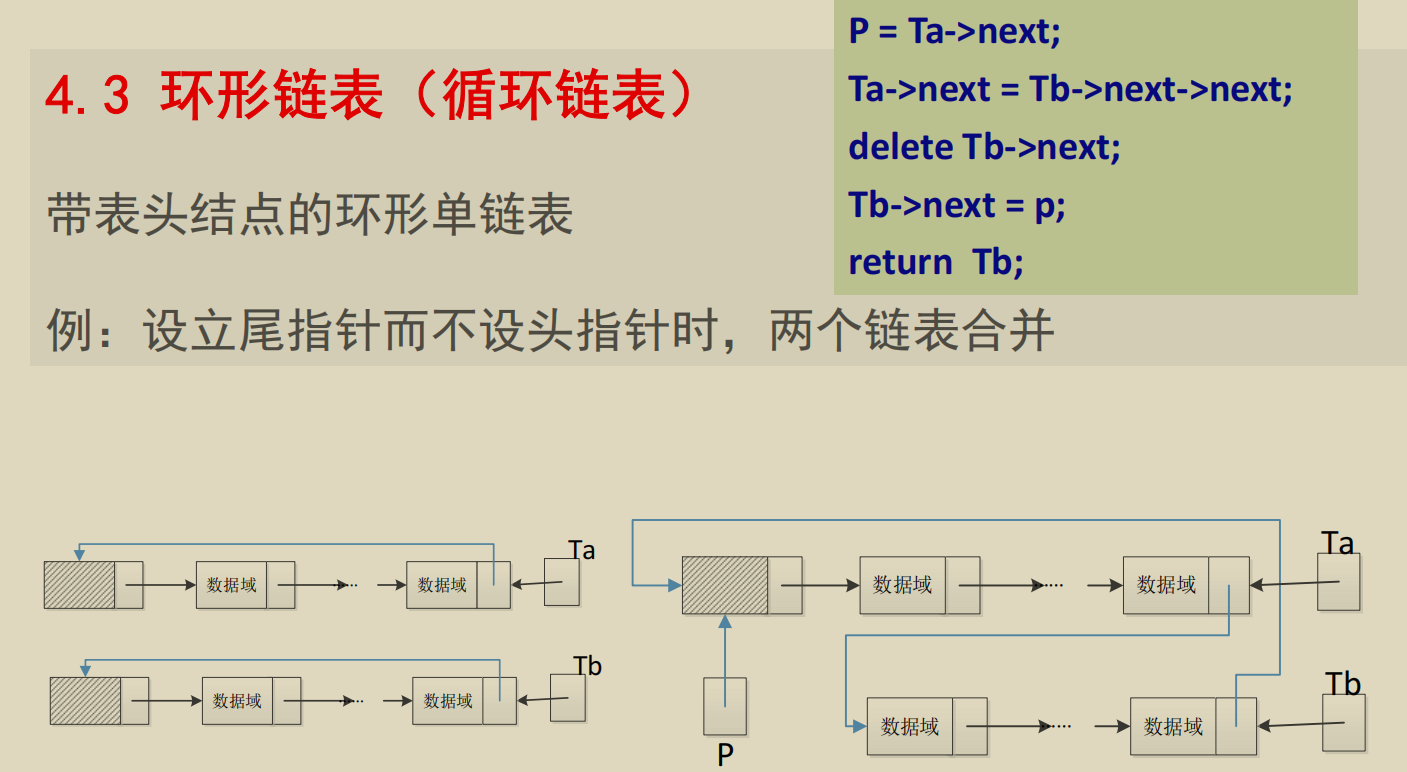
循环链表
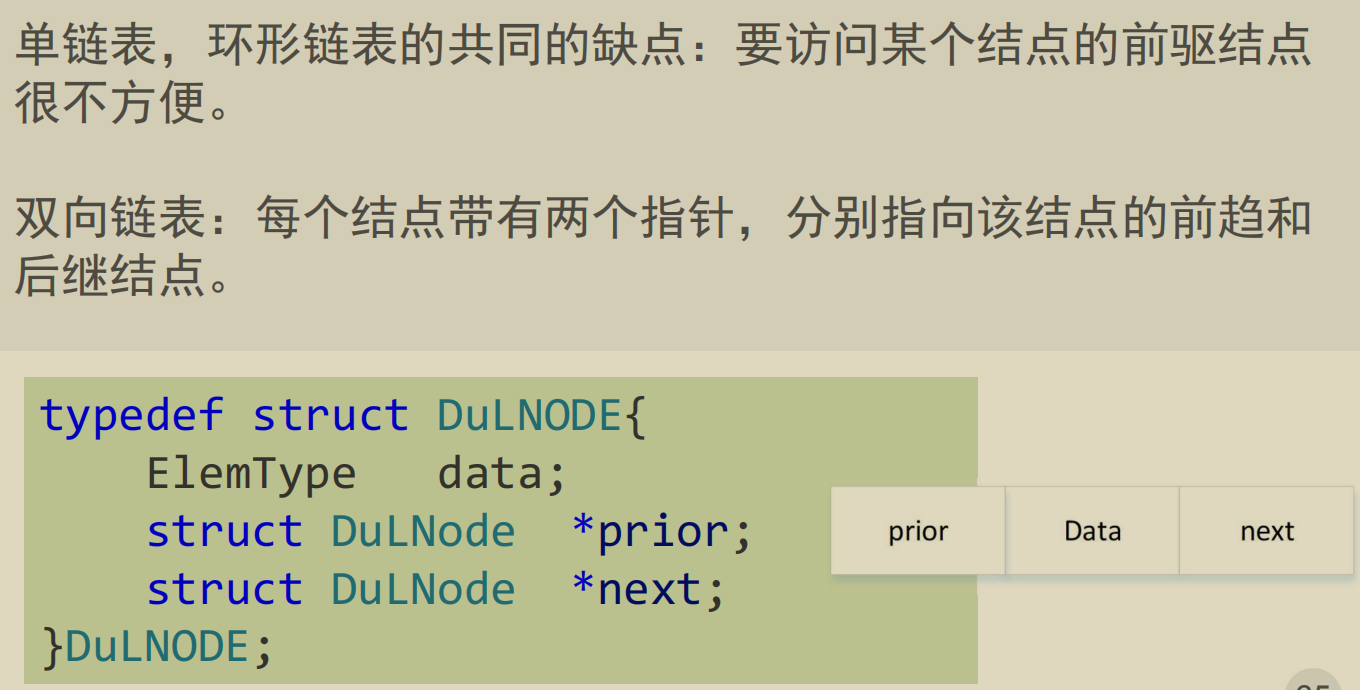
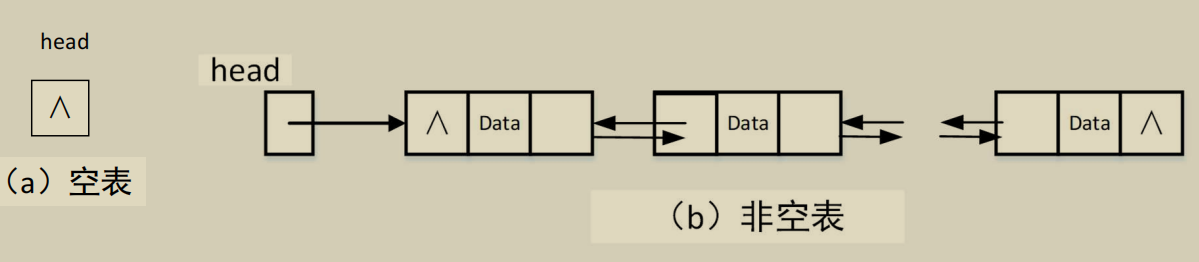
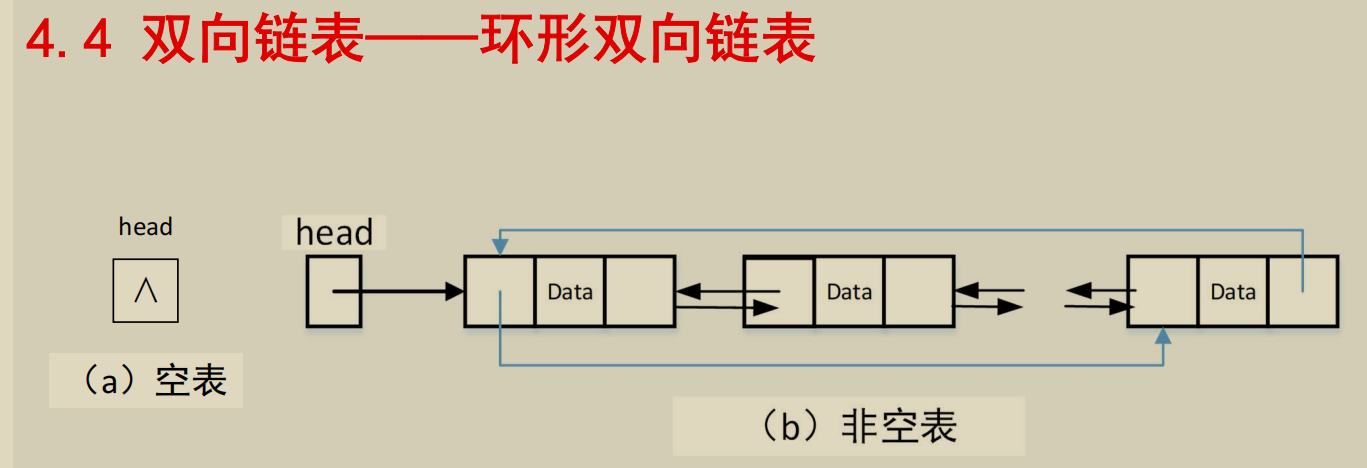
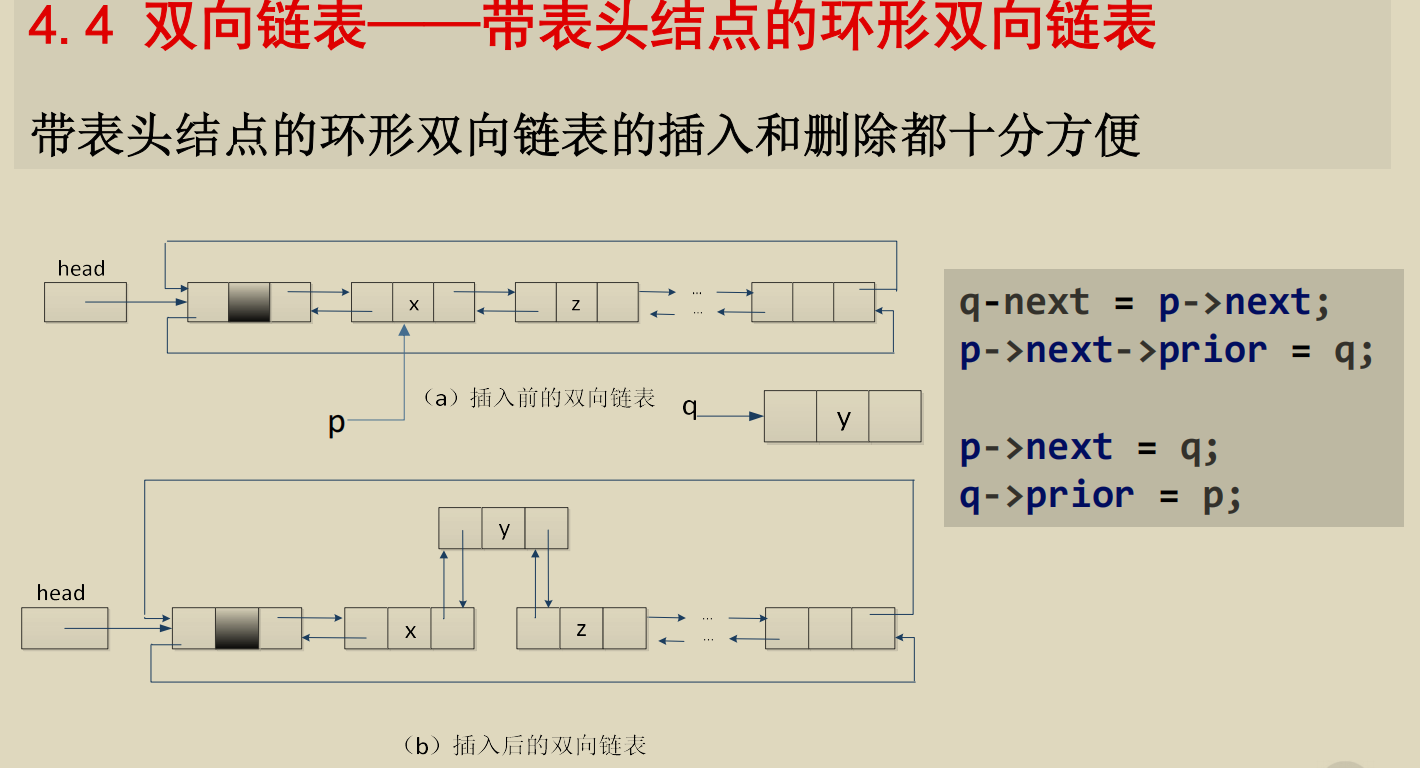
双向链表
栈和队列
栈和队列的定义和特点
这问题我一开始没看太懂, 问了 ai 才知道啥意思. 就是 ABC
是可以入栈之后立马出栈的. 因此第一个问题就是:
A入栈并出栈,B入栈并出栈,C入栈并出栈 :A, B, CA入栈并出栈,B入栈,C入栈并出栈,B出栈 :A, C,
BA入栈,B入栈并出栈,A出栈,C入栈并出栈 :B, A,
CA入栈,B入栈并出栈,C入栈并出栈,A出栈 :B, C,
AA入栈,B入栈,C入栈并出栈,B出栈,A出栈 :C, B,
A
对于 n 个元素的情况, 考虑将问题分解. 假设有 4 个元素 ABCD,
相比三个元素的情况, 多了一个 D, 那么 D 有可能是第一个出栈的, 此时就是
f(0) * 1 * f(3) (即考虑剩余三个元素出栈顺序的所有可能性),
如果是第二个出栈的, 此时就先要让一个元素出栈, 再让自己出栈,
再让剩余两个元素出栈, 所以是 f(1) * 1 * f(2). 如果是第三个出栈的,
就先让两个元素出栈, 再让自己出栈, 再让剩余的一个元素出栈, 所以是 f(2) *
1 * f(1), 同理如果是第四个出栈, 就是 f(3) * 1 * f(0).
这样, 对于 n 个元素的情况, 我们也能推广得到了:
栈的表示和实现
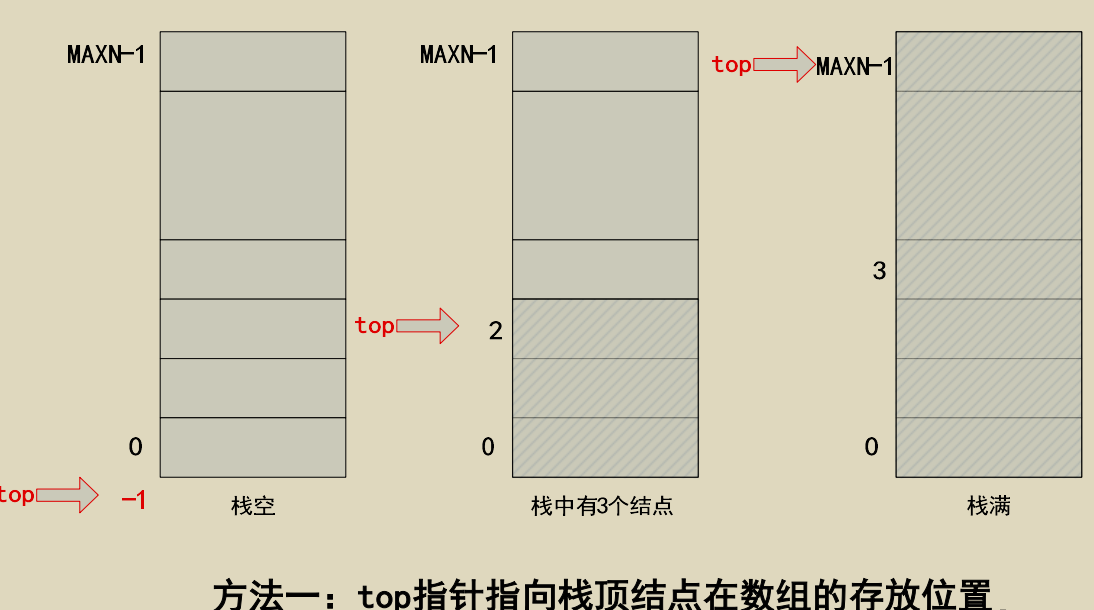
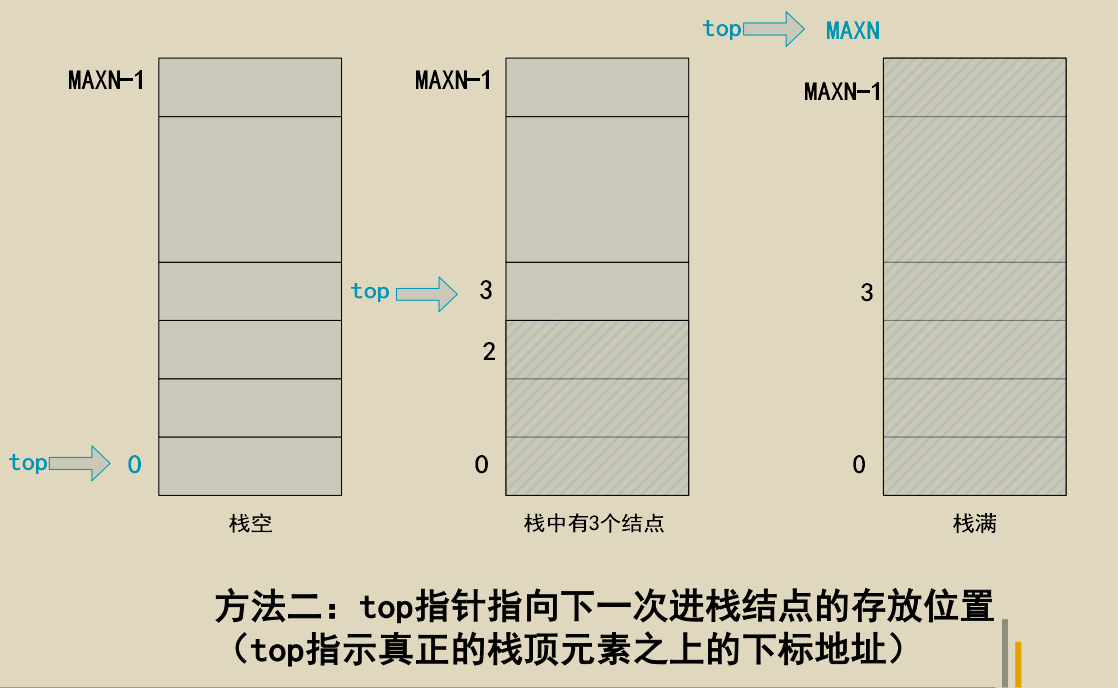
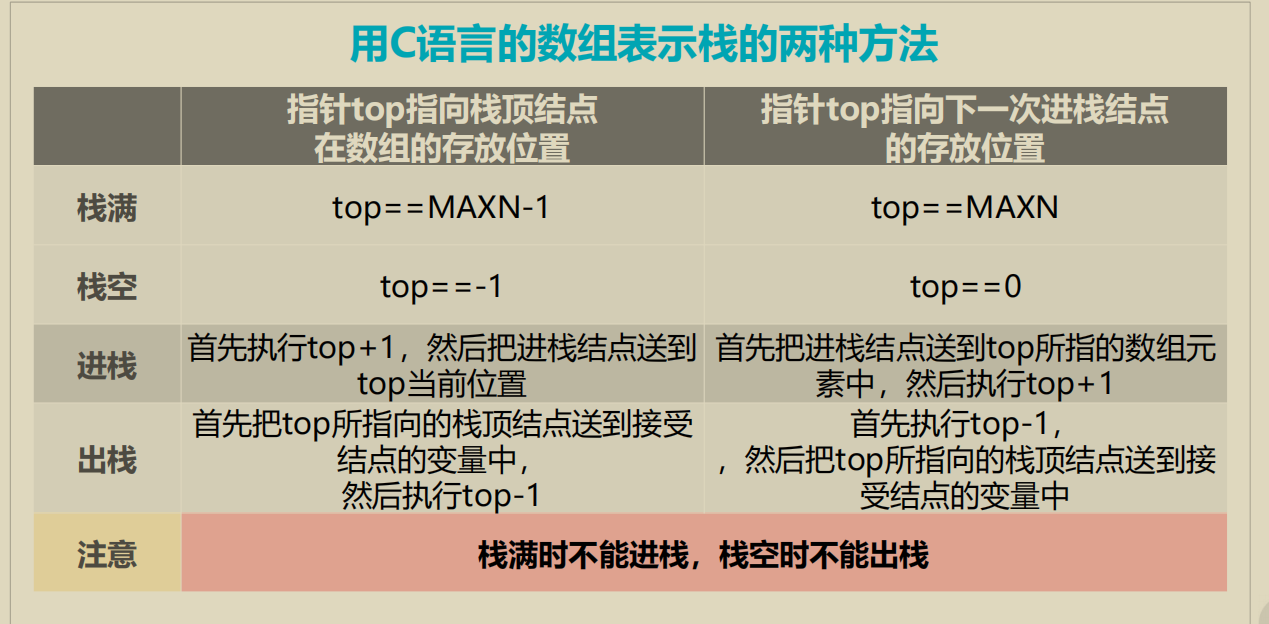
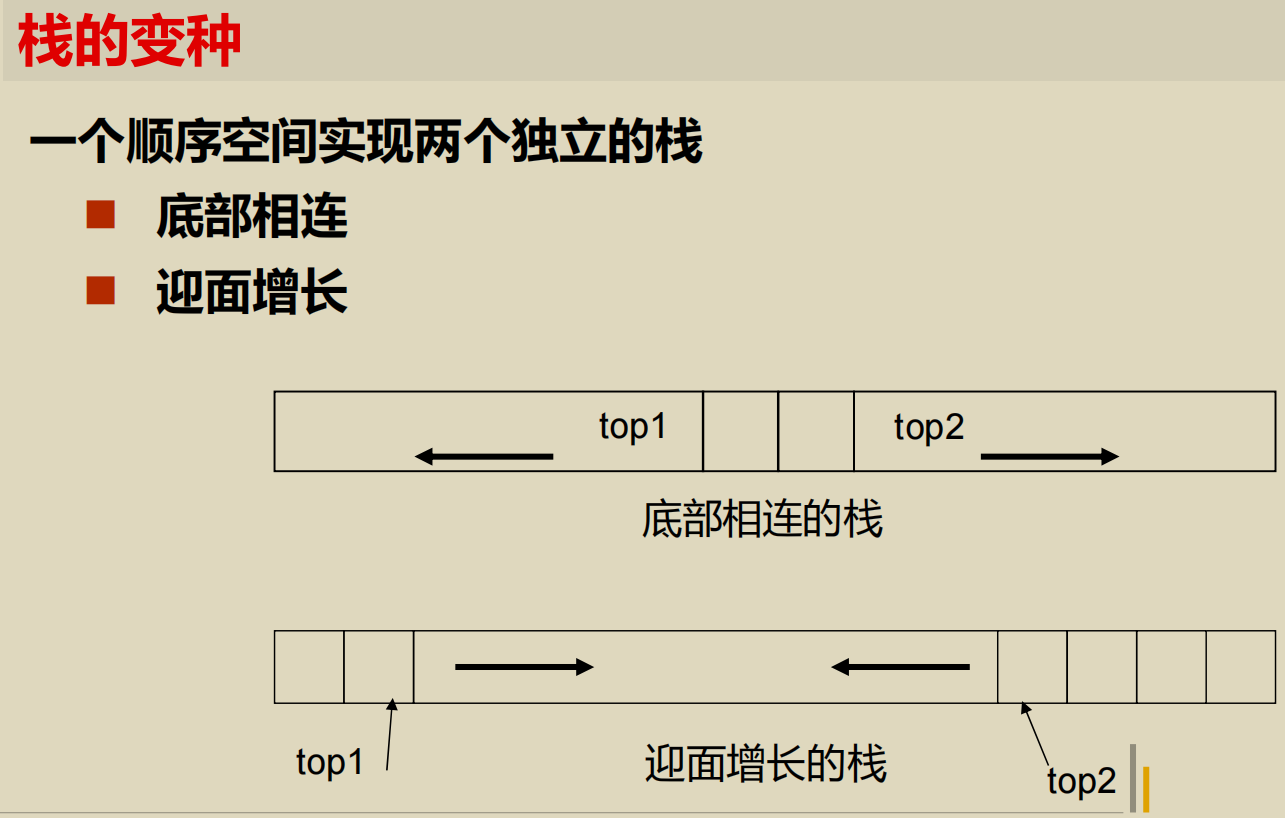
顺序栈
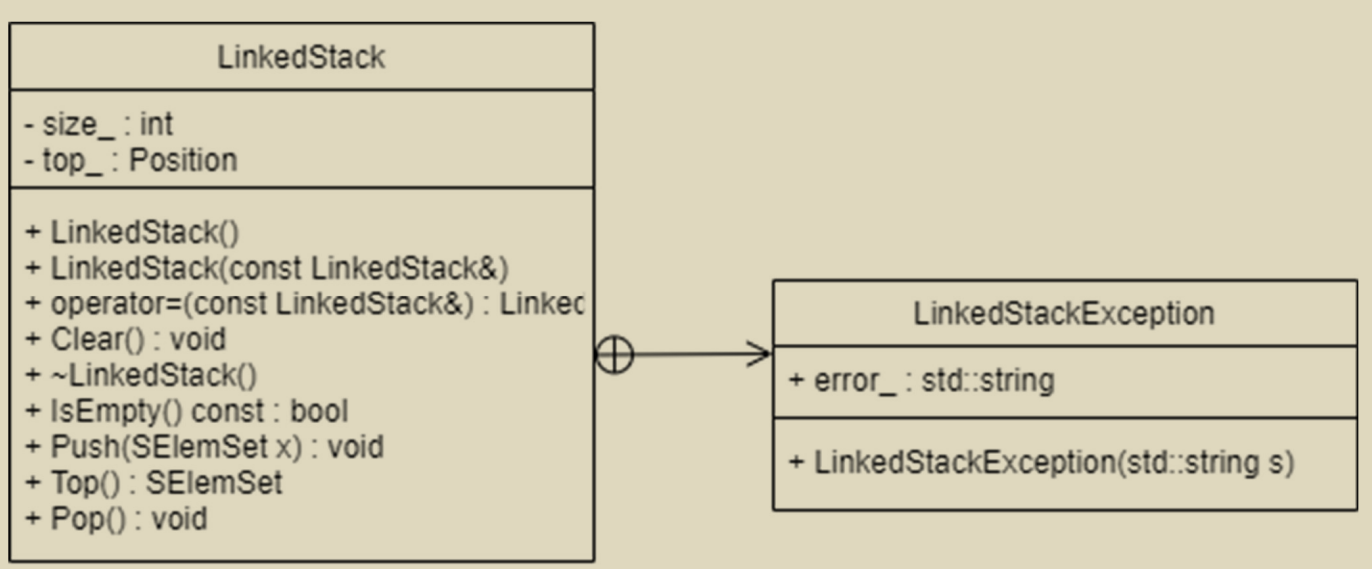
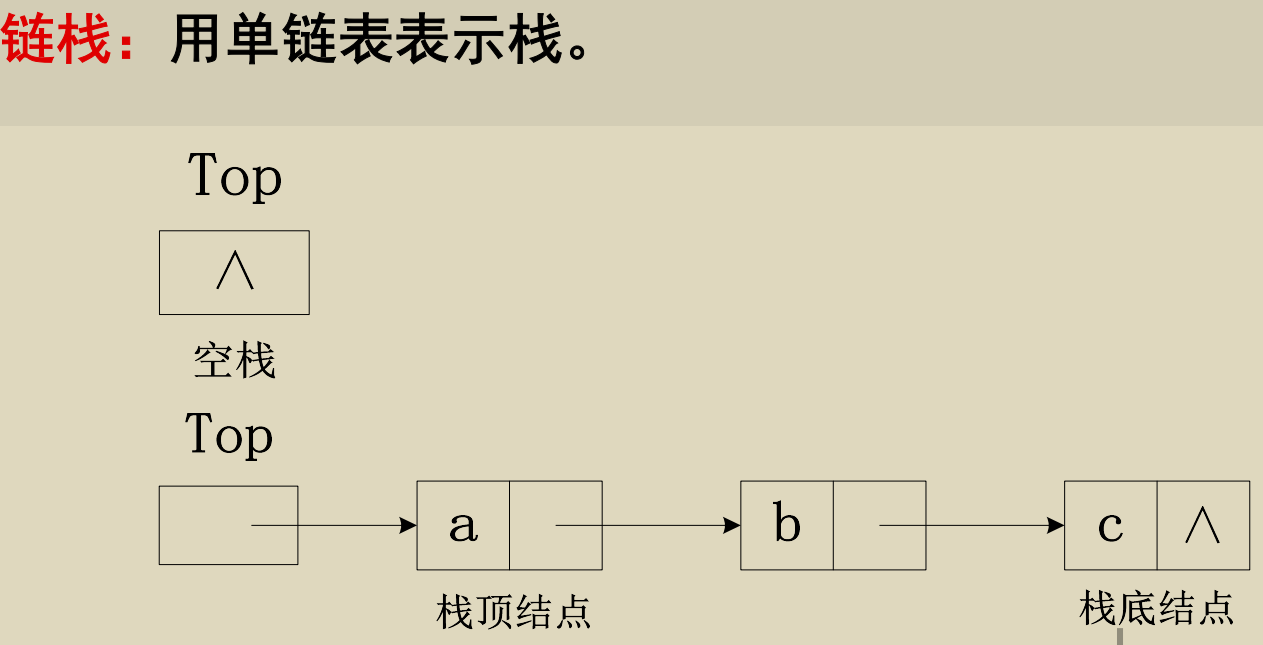
链栈
#include <iostream> #include <string> #define NIL nullptr typedef int SElemSet;typedef struct StackNode * Position; struct StackNode { SElemSet data_; Position next_; }; class LinkedStack {private : int size_; Position top_; public : struct LinkedStackException { std::string error_; explicit LinkedStackException (std::string& s) : error_(s) { }; LinkedStack (); LinkedStack (const LinkedStack&); LinkedStack& operator =(const LinkedStack&); void Clear () ~LinkedStack (); bool IsEmpty () const void Push (SElemSet x) SElemSet Top () const ; void Pop () void DestoryLinkedStack () };
void LinkedStack::Push (SElemSet x) Position new_node; new_node = new StackNode{ x, top_ }; top_ = new_node; size_++; } void LinkedStack::Pop () Position temp; if (IsEmpty ()) { printf ("错误:栈为空。\n" ); } else { temp = top_; top_ = top_->next_; delete temp; size_--; } }
队列的表示和实现
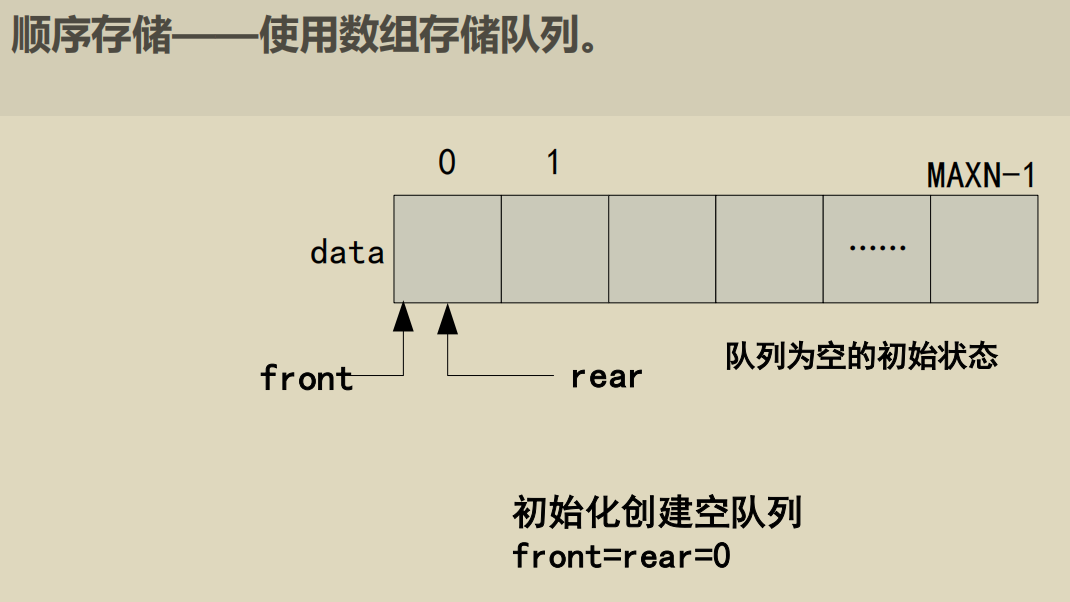
顺序队列
这里注意不要理解错了, rear 的元素是后加入的元素.
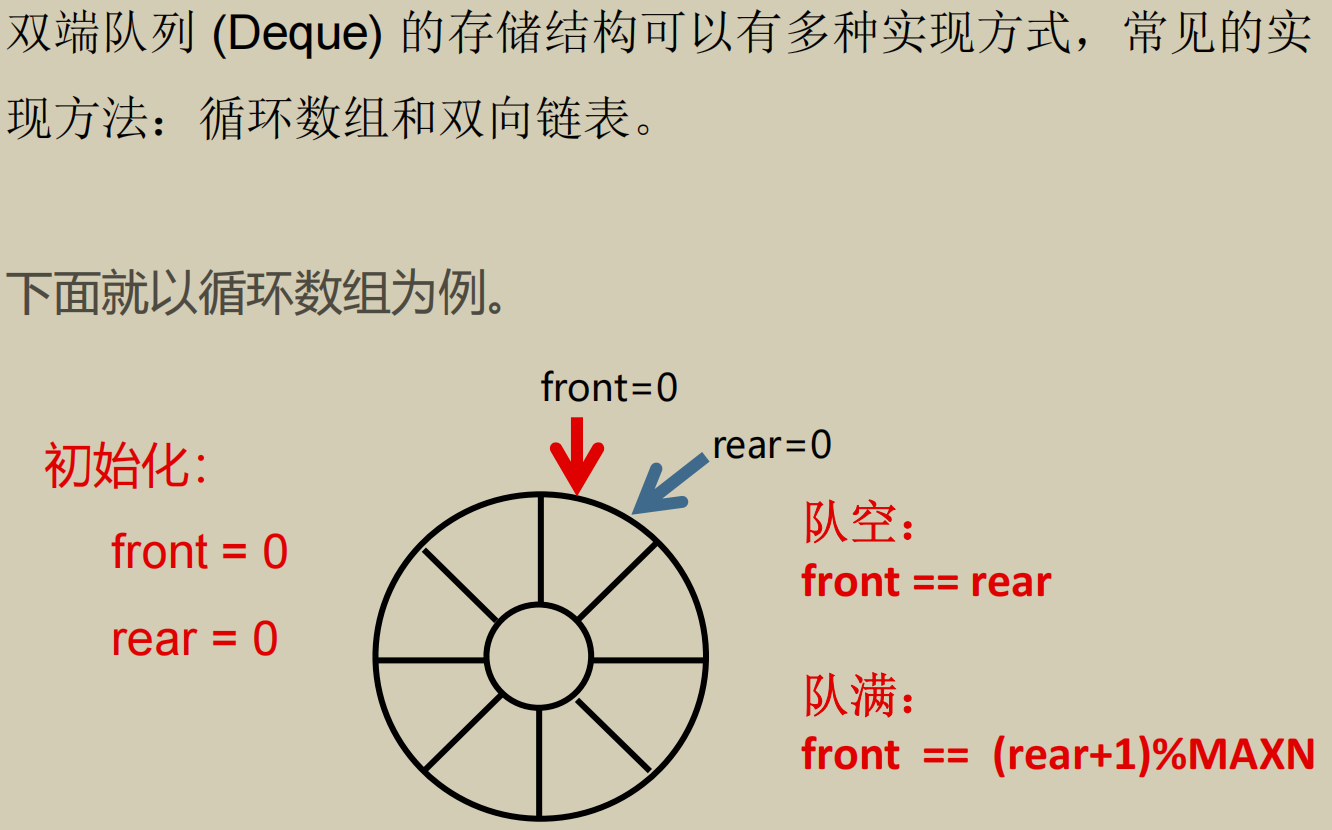
这里假溢出其实值得就是 front 和 rear 靠的很近, 但是 rear 指向 max
导致此时无法进行入队操作.
这里第二个等式可以想象一个例子: 当 rear 指向 maxn - 1, front 指向 0,
此时肯定是满的. 为了让这时候判定为满, 用上面的等式就可以了.
这里对 rear 的赋值还是要注意的. "循环后继"操作.
链队
这里在队首插入元素和删除队尾元素的操作有点抽象了. 实际上比如 front =
(front - 1 + capacity) % capacity; 这个操作, 是防止在 front = 0
的时候在队首插入元素时让 front 变成负. 对于 front != 0
的情况其实加上一个 capacity 没有任何影响.
栈和队列的应用
死去的 scheme 在攻击我...
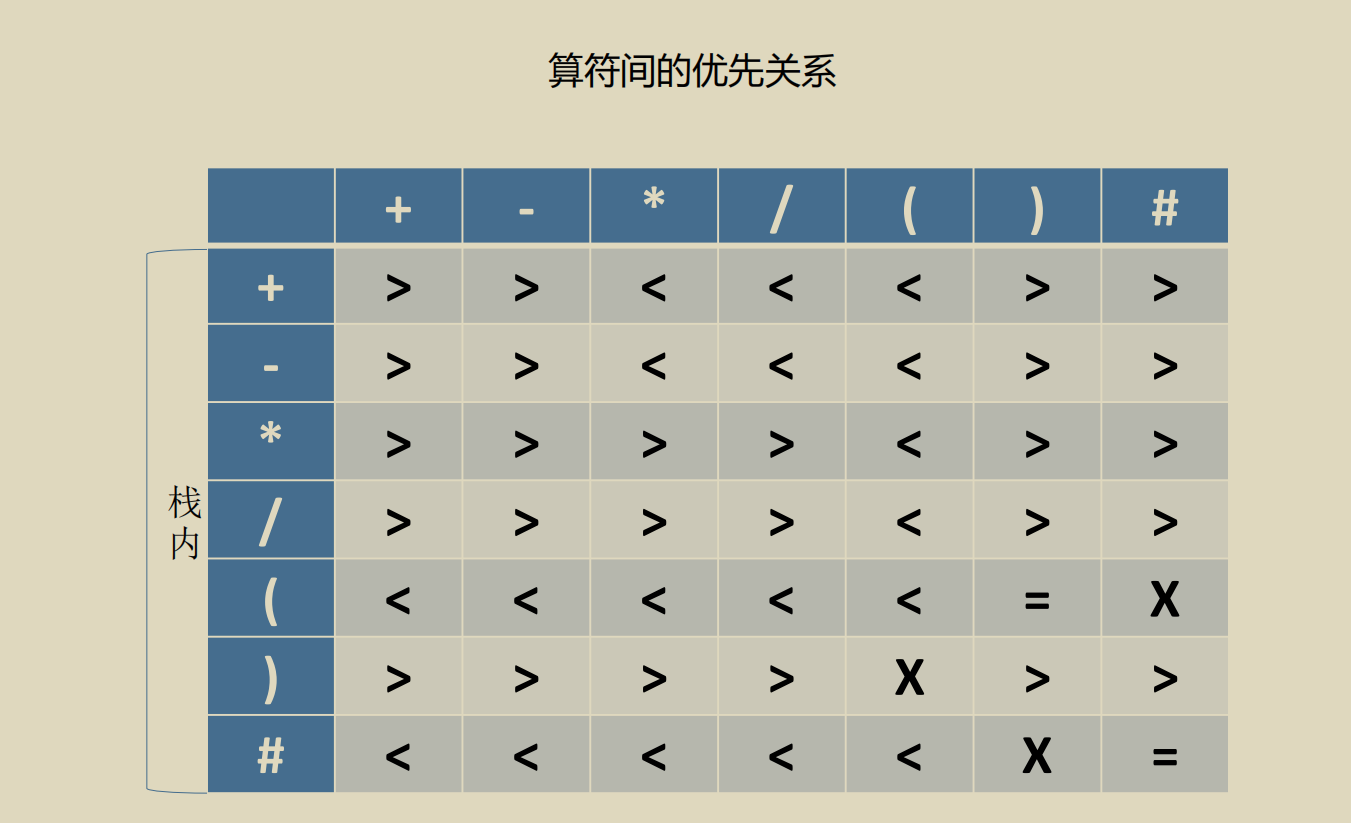
如果新读入的运算符的优先级更低, 就出栈进行运算,
如果更高就继续入栈.
注意, 只有括号和#之间优先级时相同的.
只能说思路真巧妙...
#include <iostream> #include <vector> #include <stack> using namespace std;const int directions[8 ][2 ] = { {-1 , -1 }, {-1 , 0 }, {-1 , 1 }, {0 , -1 }, {0 , 1 }, {1 , -1 }, {1 , 0 }, {1 , 1 } }; bool dfs (vector<vector<int >>& maze, vector<pair<int , int >>& path, int i, int j, pair<int , int > end) int rows = maze.size (); int cols = maze[0 ].size (); if (i == end.first && j == end.second) { path.push_back ({i, j}); return true ; } maze[i][j] = 1 ; path.push_back ({i, j}); for (const auto & dir : directions) { int ni = i + dir[0 ]; int nj = j + dir[1 ]; if (ni >= 0 && ni < rows && nj >= 0 && nj < cols && maze[ni][nj] == 0 ) { if (dfs (maze, path, ni, nj, end)) { return true ; } } } path.pop_back (); return false ; } void solve_maze (vector<vector<int >>& maze, pair<int , int > start, pair<int , int > end) vector<pair<int , int >> path; if (dfs (maze, path, start.first, start.second, end)) { cout << "Path found:" << endl; for (const auto & p : path) { cout << "(" << p.first << ", " << p.second << ")" << endl; } } else { cout << "No path found." << endl; } } int main () vector<vector<int >> maze = { {0 , 1 , 0 , 0 , 0 }, {0 , 1 , 0 , 1 , 0 }, {0 , 0 , 0 , 1 , 0 }, {0 , 1 , 1 , 1 , 0 }, {0 , 0 , 0 , 0 , 0 } }; pair<int , int > start = {0 , 0 }; pair<int , int > end = {4 , 4 }; solve_maze (maze, start, end); return 0 ; }
ds 给出的代码, 用作参考吧.


















































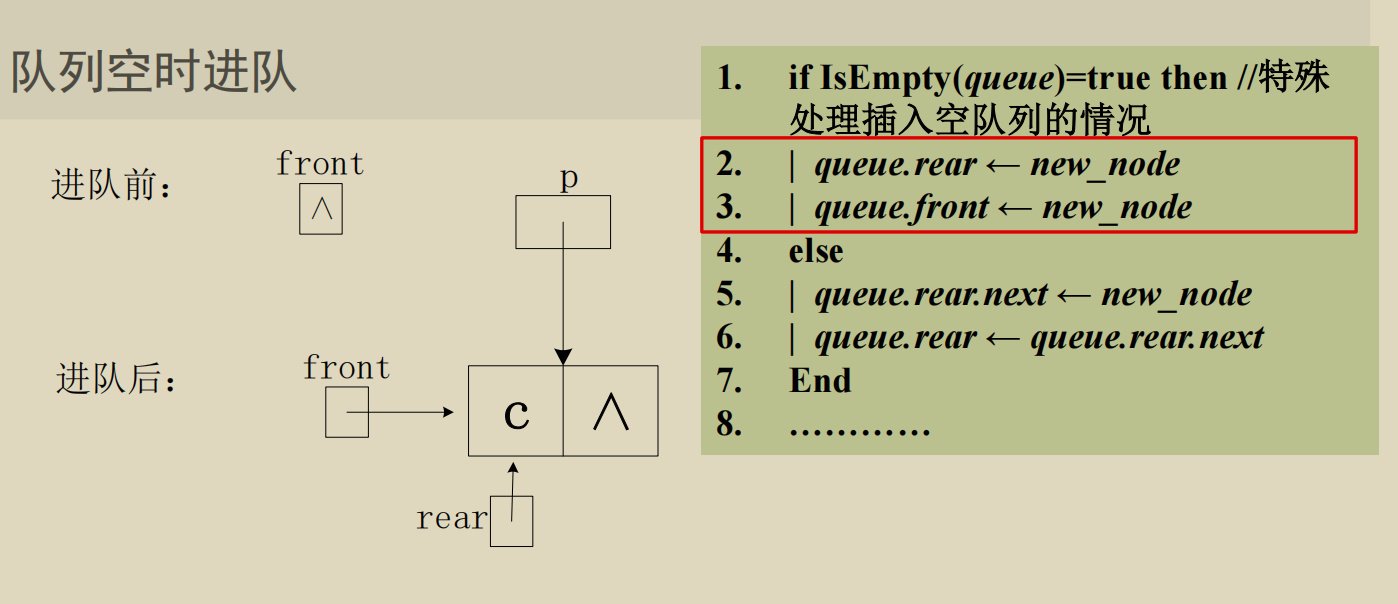
 同样地, 对 front 的赋值也要特殊处理.
同样地, 对 front 的赋值也要特殊处理.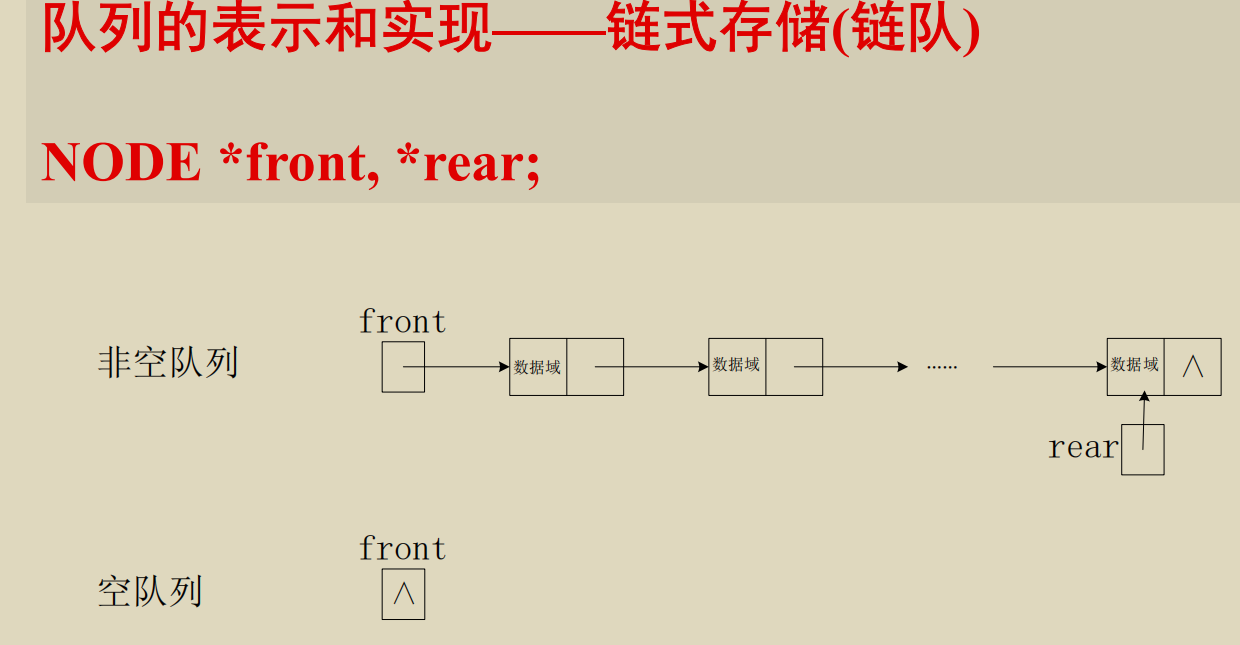
































.jpg)
