[笔记]光线追踪(games101)
Whitted Style Raytracing
从相机出发, 朝某个像素点出射光线, 直到接触到的第一个物体的位置, 从该位置与光源连线, 若连线上没有其他物体, 说明该点可以被照亮. 此时使用布林冯等着色模型进行着色即可.
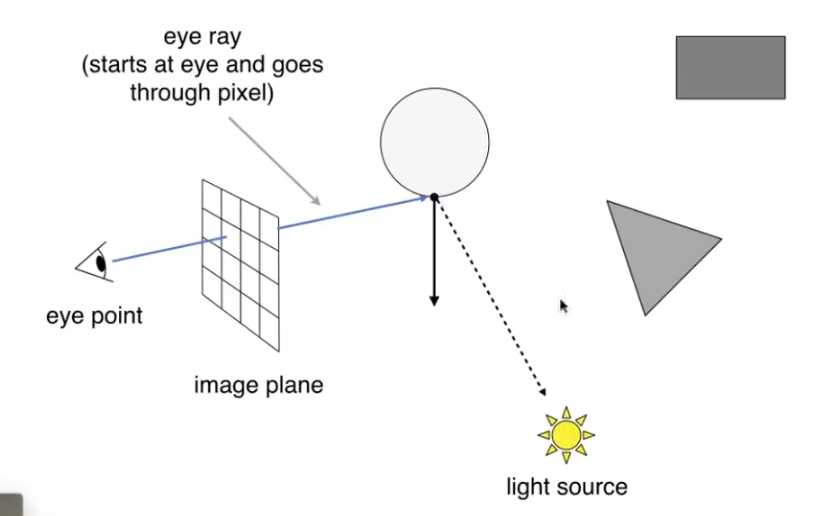
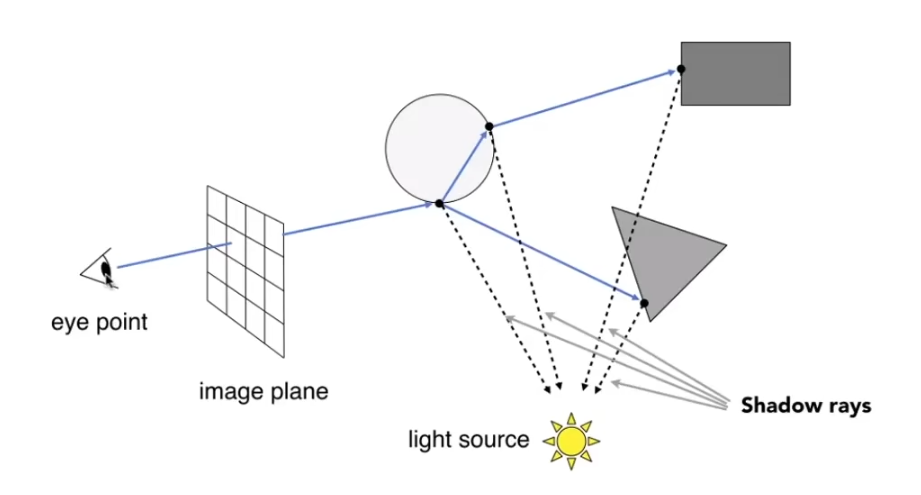
同时考虑折射, 反射, 最后将所有点的贡献叠加, 作为当前像素的着色结果.
求光线与表面的交点
在这里说的光线应该指的是从相机射出的光线.
数学上的光线表示为: 从某点延申的一条射线.
球的表面表示为: 表面上的点到圆心的距离等于半径. 注意向量的平方是个标量.
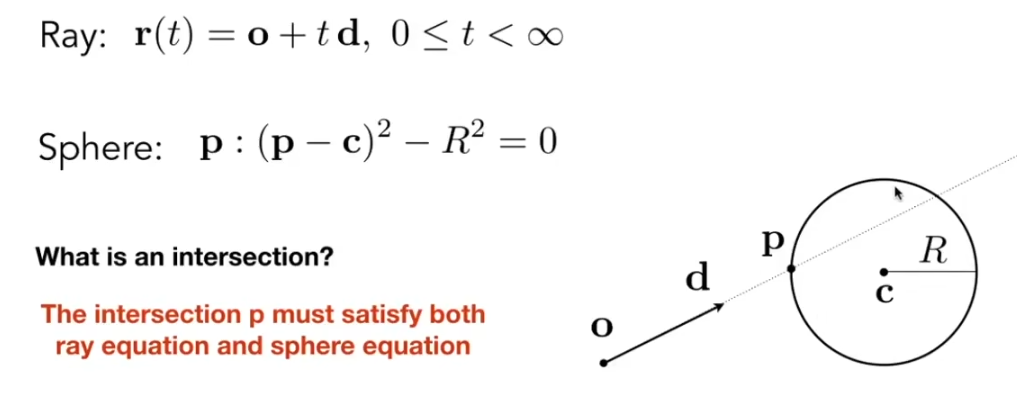
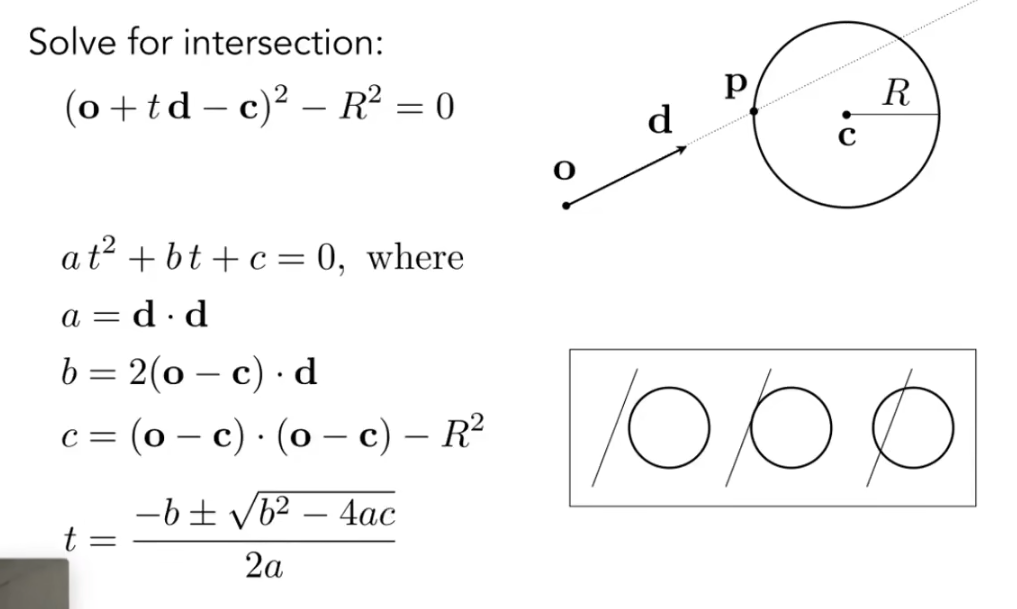
代入解出t. 注意t必须是正的. 解的数量决定交点数量.
对于一般的隐式表面:

解出t之后, 那交点的位置其实就在o + td.
这里说下隐式表面和显示表面的区别. 前者代表满足某个方程的点. 后者则是给定参数, 用参数生成表面方程.
对于显示表面求交, 我们侧重的一般是与三角形面求交. 这个问题又能分解为先判断是否与三角形所在平面求交, 然后再判断是否与三角形求交.
一个平面, 我们只需要用一个法线和一个点即可定义. 这个被定义的平面与法线垂直, 并且过这个点.

联立方程求解.
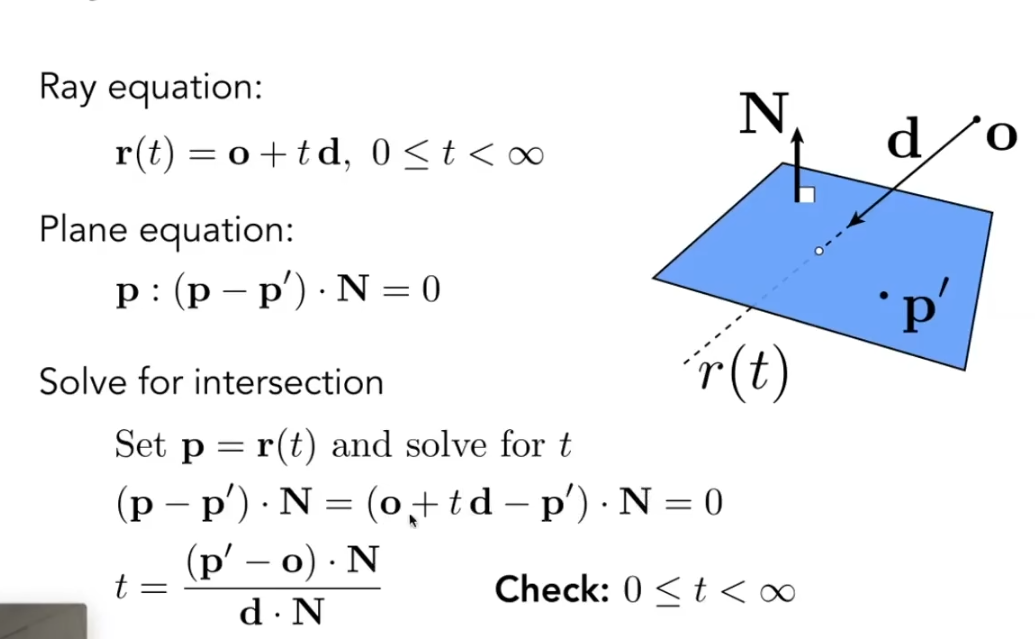
解出交点后, 再判断是否在三角形内即可.
另一种, 能够一次性解出相交情况的算法: MT算法.
简单来说, 光线依旧是那个o + td, 但是我们用重心坐标形式的三角形平面表示法, 然后联立. 三个未知数, 而向量又是三维的因此有三个方程, 解线性方程组即可.

加速光线表面求交
上面提到的光线与表面求交, 使用在与模型的所有三角形面进行求交. 这样速度很慢, 我们希望提高计算速度.
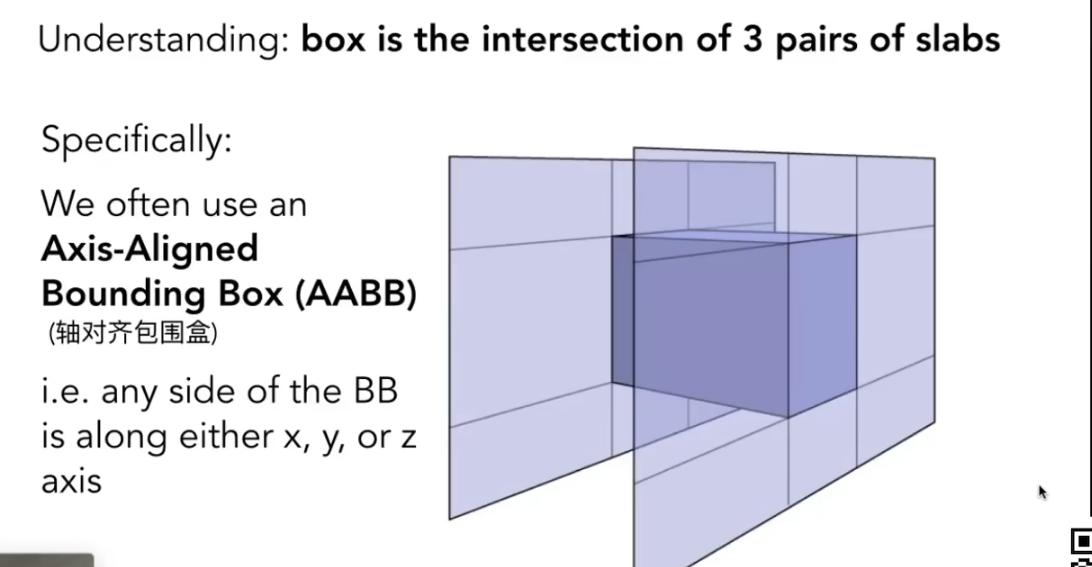
包围盒(bounding volumes): 用简单的体积包围一个复杂的物体. 如果连包围盒都碰不到, 那么光线不可能与物体表面相交.

我们常用的是AABB(轴对齐包围盒). 一个包围盒认为是三个相对平面围成的长方体.
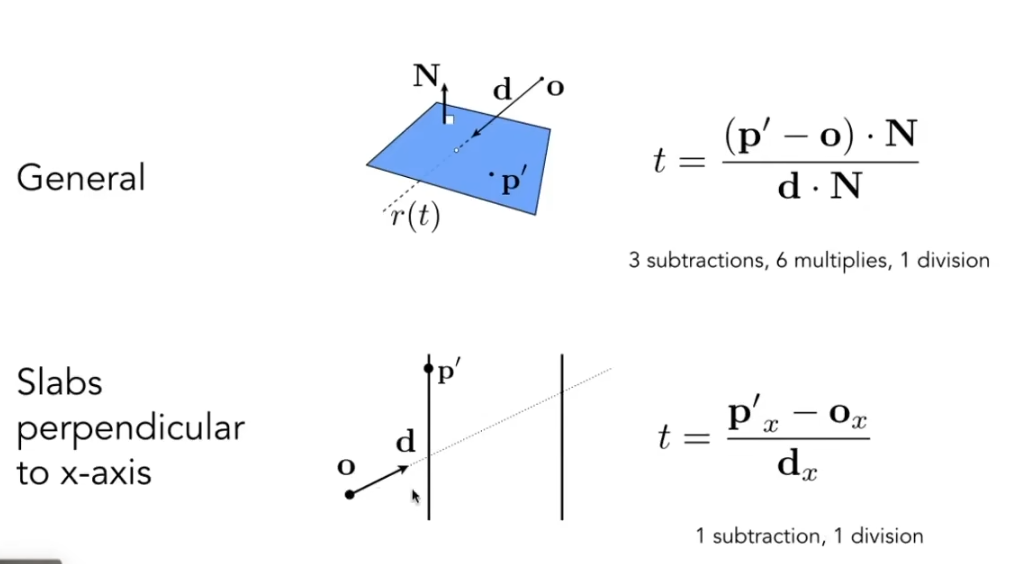
分别在x, y, z方向上, 一共六个平面, 用前面光线求交的方式, 可以求出六个t, 我们选择最大的tmin和最小的tmax, 就能得到光线经过这个包围盒的入射时间和出射时间.,

我们就在进入时间和退出时间上做文章. 如果退出时间为负的, 那么这个包围盒在光源背后, 没有交点; 如果退出时间为正而进入时间为负, 那么光源必定在包围盒之内, 必有交点. 所以相交当且仅当进入时间小于离开时间且离开时间大于等于0

最后, 在计算射线与包围盒交点的时候, 可以使用分量计算, 更快速简洁.
加速结构
基础的加速结构:
首先得到包围盒, 然后在包围盒内部创建网格, 存储每个物体覆盖的小网格.
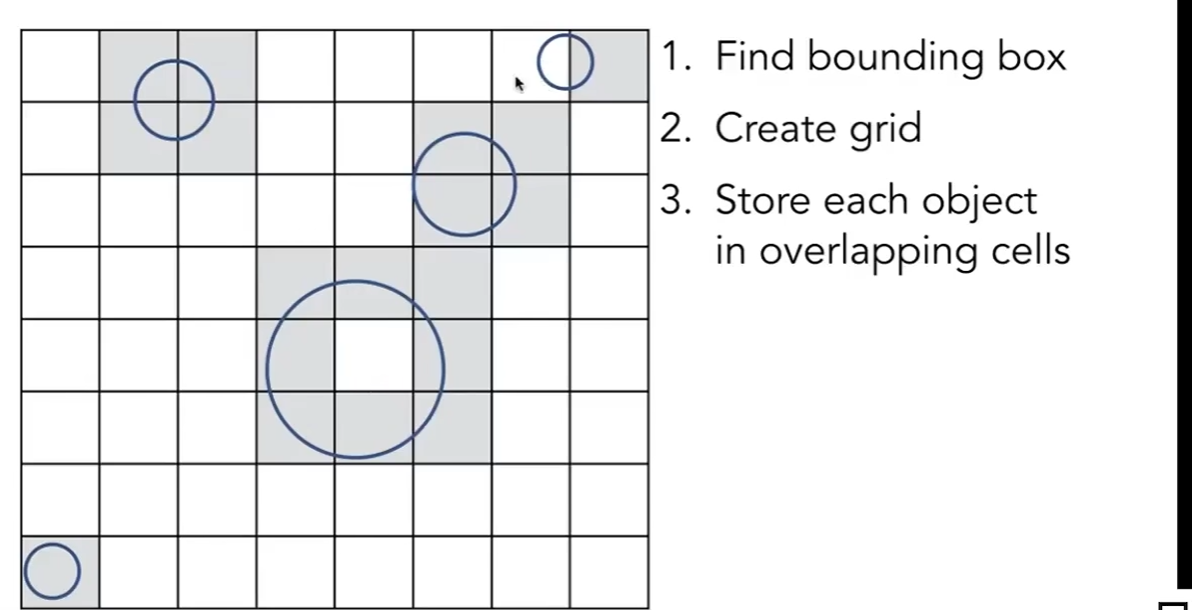
然后光线遍历网格, 在达到被物体覆盖的网格后, 与物体进行求交计算.
光线行进时无需遍历所有网格, 会采用类似画线算法的思路来计算.
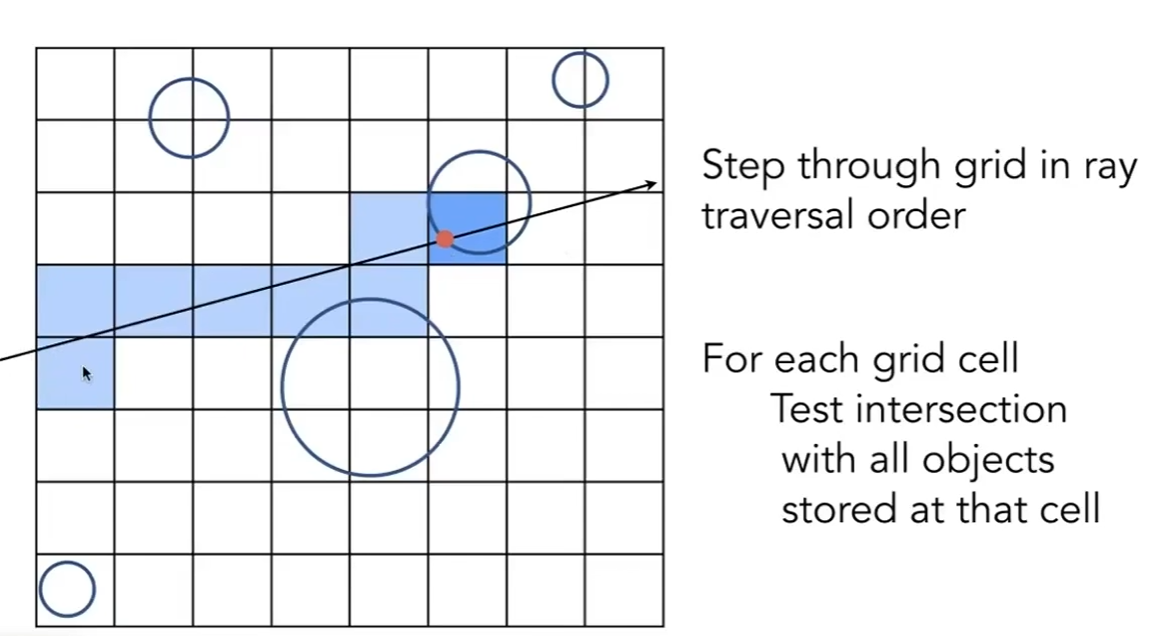
在物体分布均匀的场景中, 这种方法的效果比较好.

分布不均匀的场景, 效果欠佳. 有大部分网格被浪费掉.

空间划分
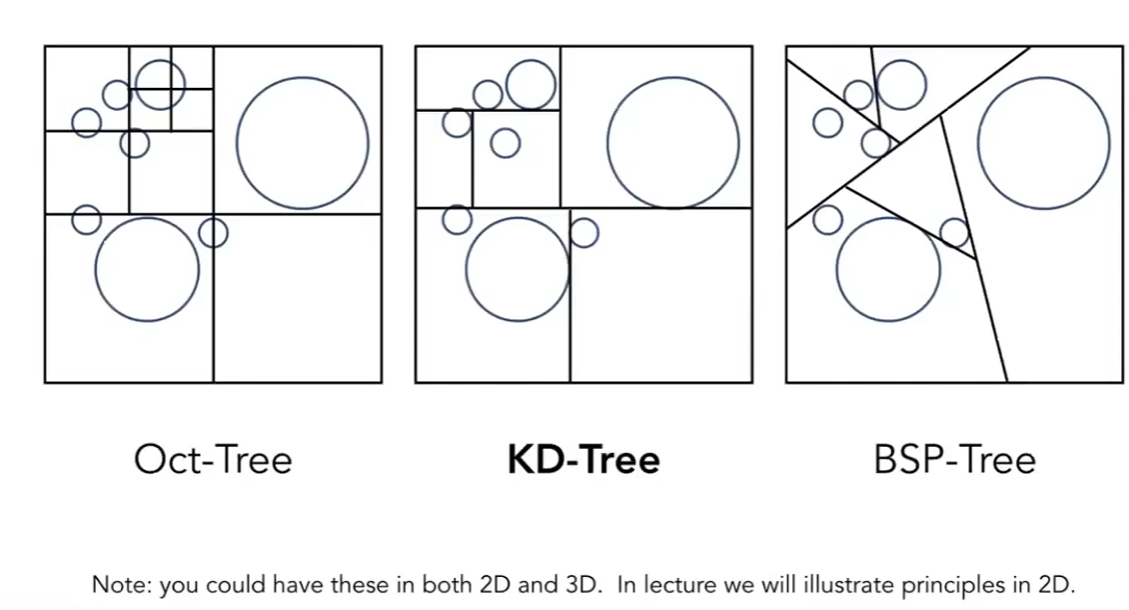
第一个是八叉树. 实际上只是示意图. 第一个图首先将空间切成八块, 然后每个子块继续切, 如果得到的子块中没有任何物体那就不需要再切了.
但是八叉树本身随着维度的升高, 指数级增长.
KD-tree则是一个不受维度影响的划分方式. 划分方式为: 给定一个网格, 先水平划分, 然后每个子块竖直划分, 然后每个子块水平划分, 以此类推. 当然这是二维的情况. 三维情况就是先沿着x, 再沿着y, 最后沿着z划分.
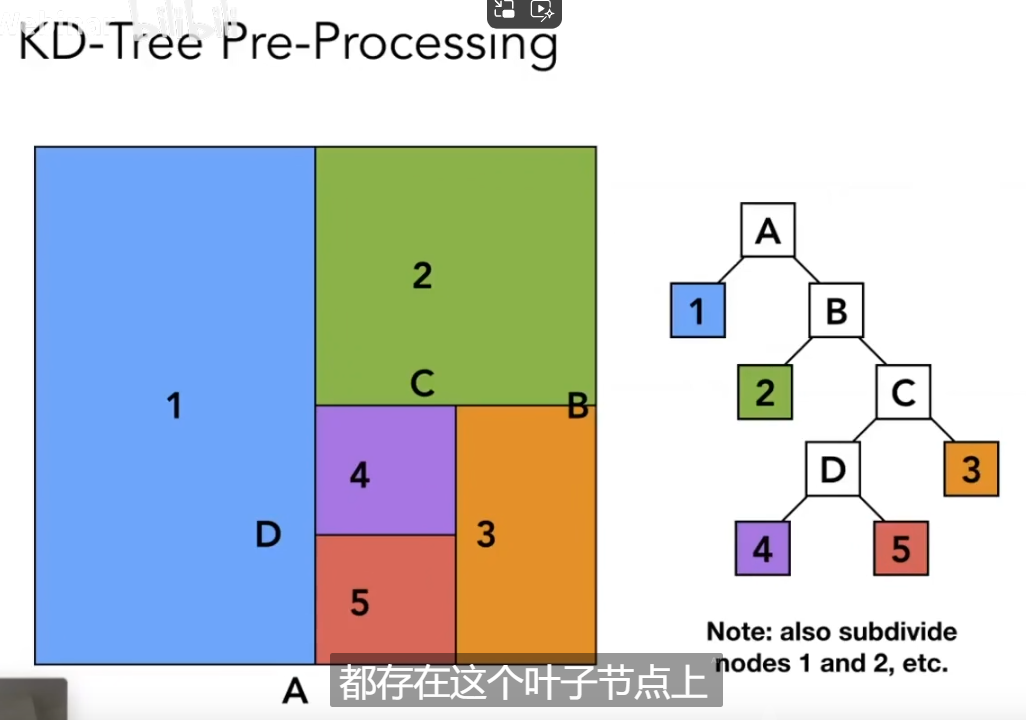
在划分之后, 具体的几何形体则会存储在叶子节点.

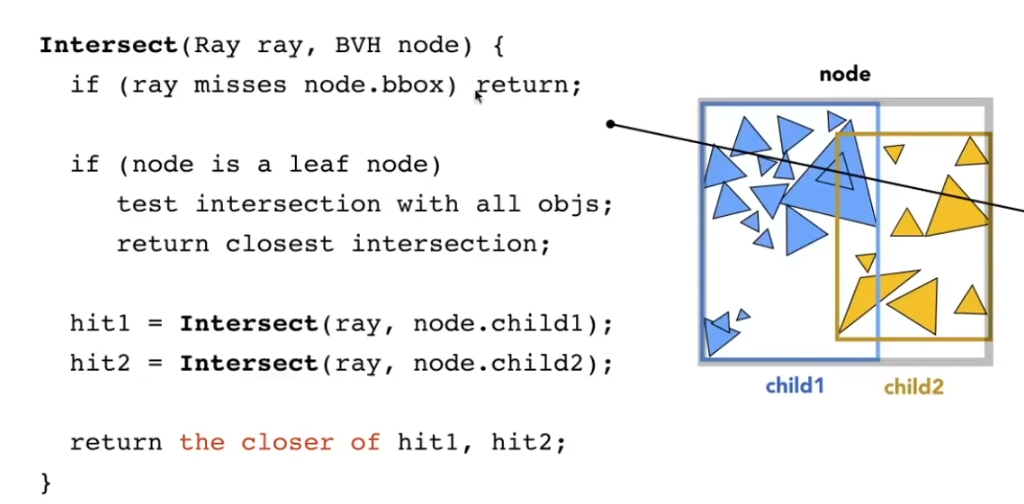
光线首先判断是否与最外层的包围盒有交点, 如果有, 那么看是否与子包围盒有交点, 遍历下去, 如果遍历到了叶子节点对应的网格后与该网格相交, 那么光线就会与网格内的所有物体求交. 在下面这张图中, 光线会与1234四个网格内的物体求交, 不会与5网格内的物体求交.
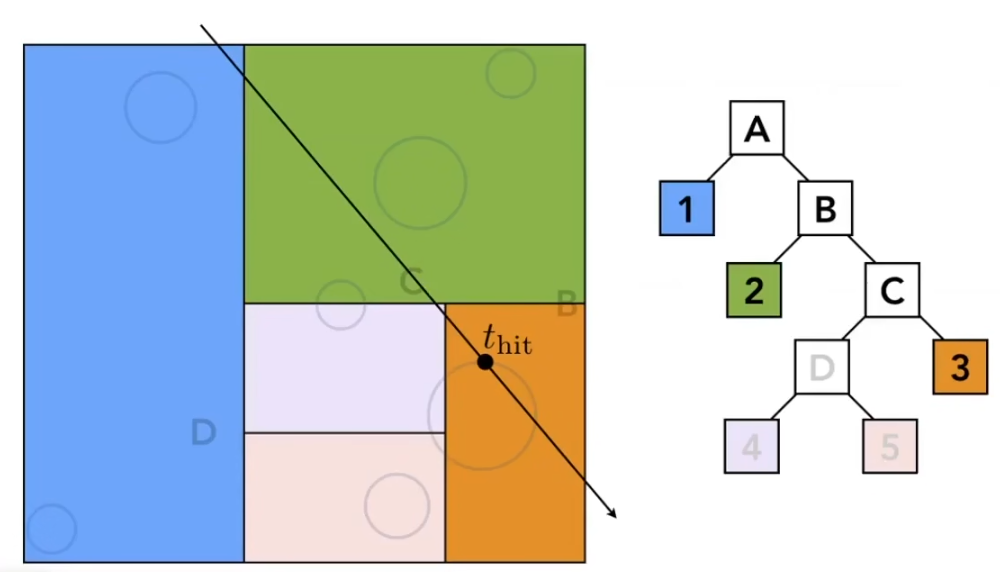
问题在于, 我们很难判定包围盒是否与三角形面有交集.
另外, 我们希望一个物体只属于一个包围盒, 而非多个包围盒共享一个物体.
所以另一个思路是基于物体划分, 而非基于空间划分.
物体划分

这种加速结构就是BVH. 现在基本上用的都是BVH.
将空间中的三角形进行划分, 然后求它们的包围盒, 这都很容易. 最后生成了多个包围盒.
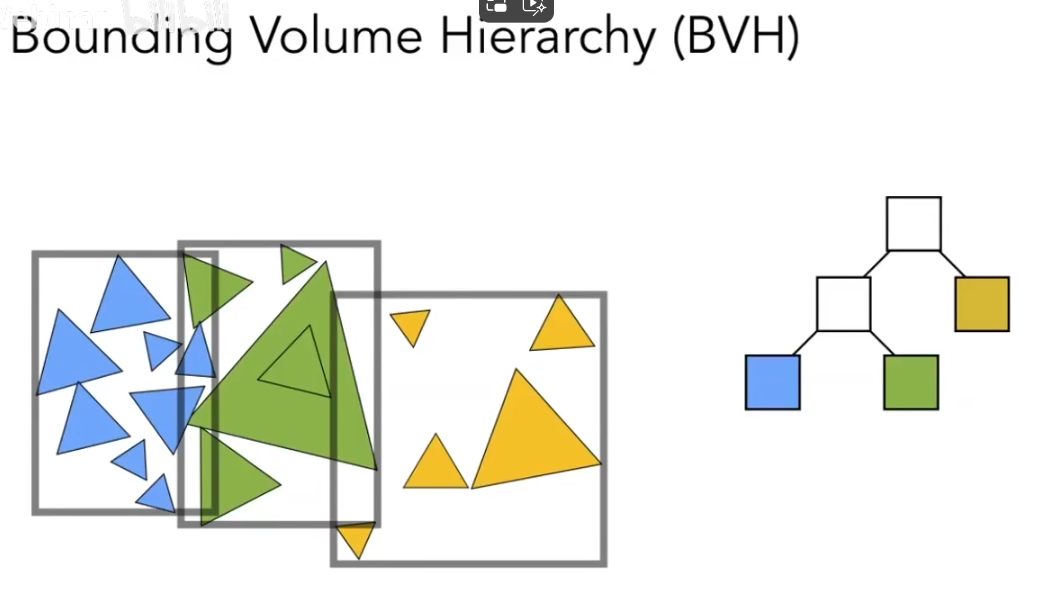
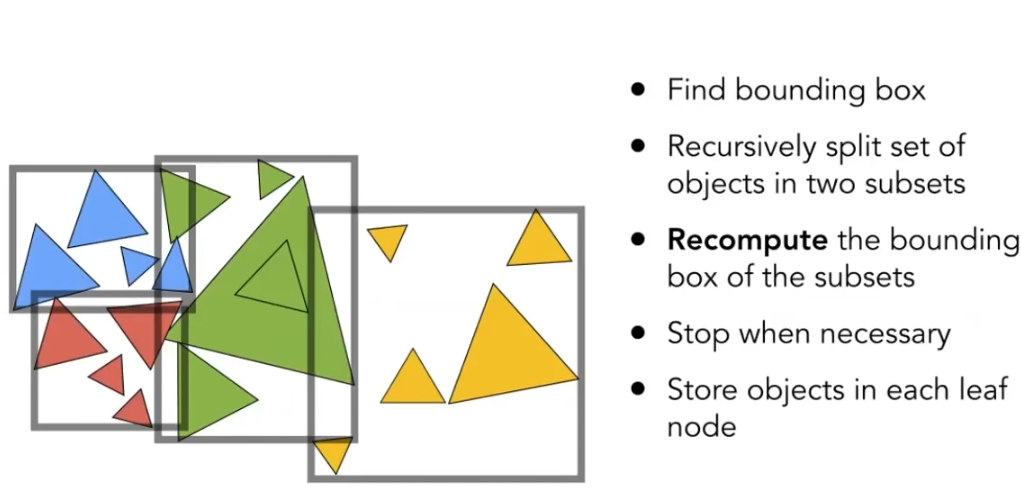
注意一下每次划分之后都要重新计算一下当前节点的包围盒.
我们希望尽可能减少包围盒的重叠, 即重点在于三角形的划分方式.
为了让划分更加均匀. 有个方法是每次只沿着最长的轴划分. 也可以每次沿着xyz. 另外一个方法就是从中位数的物体划分. 这样能够让树更平衡.
找中位数的方法可以使用快速选择算法.
如果物体动了, 那必须重新计算BVH.
渲染方程
辐射度量学
基于几何光学. 不考虑光的波动性.
--radient energy: Q, 单位是J.
--radient flux: 功率. 单位是W.
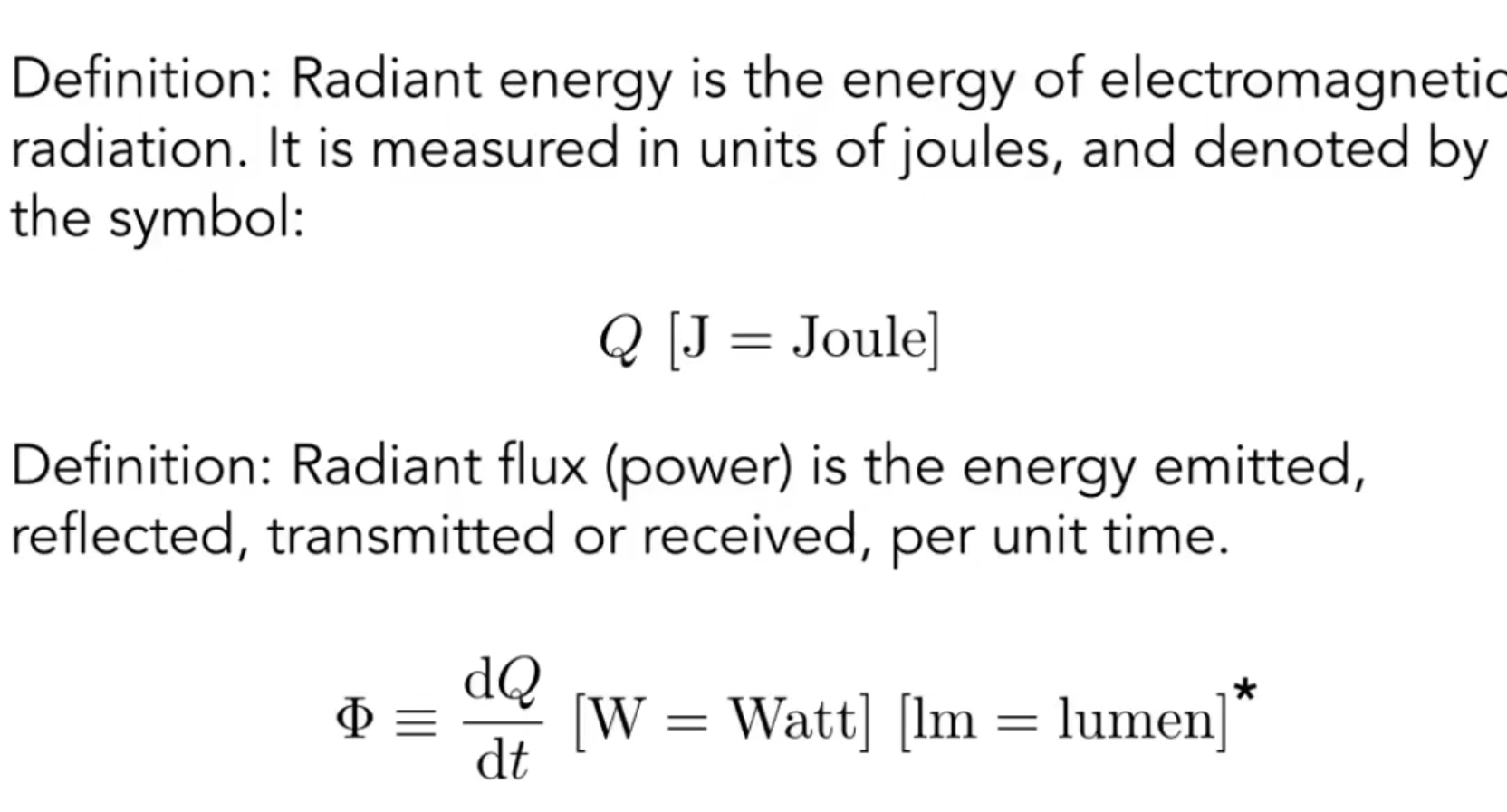
--intensity: flux沿着每个立体角的分flux. 单位是cd(candela)
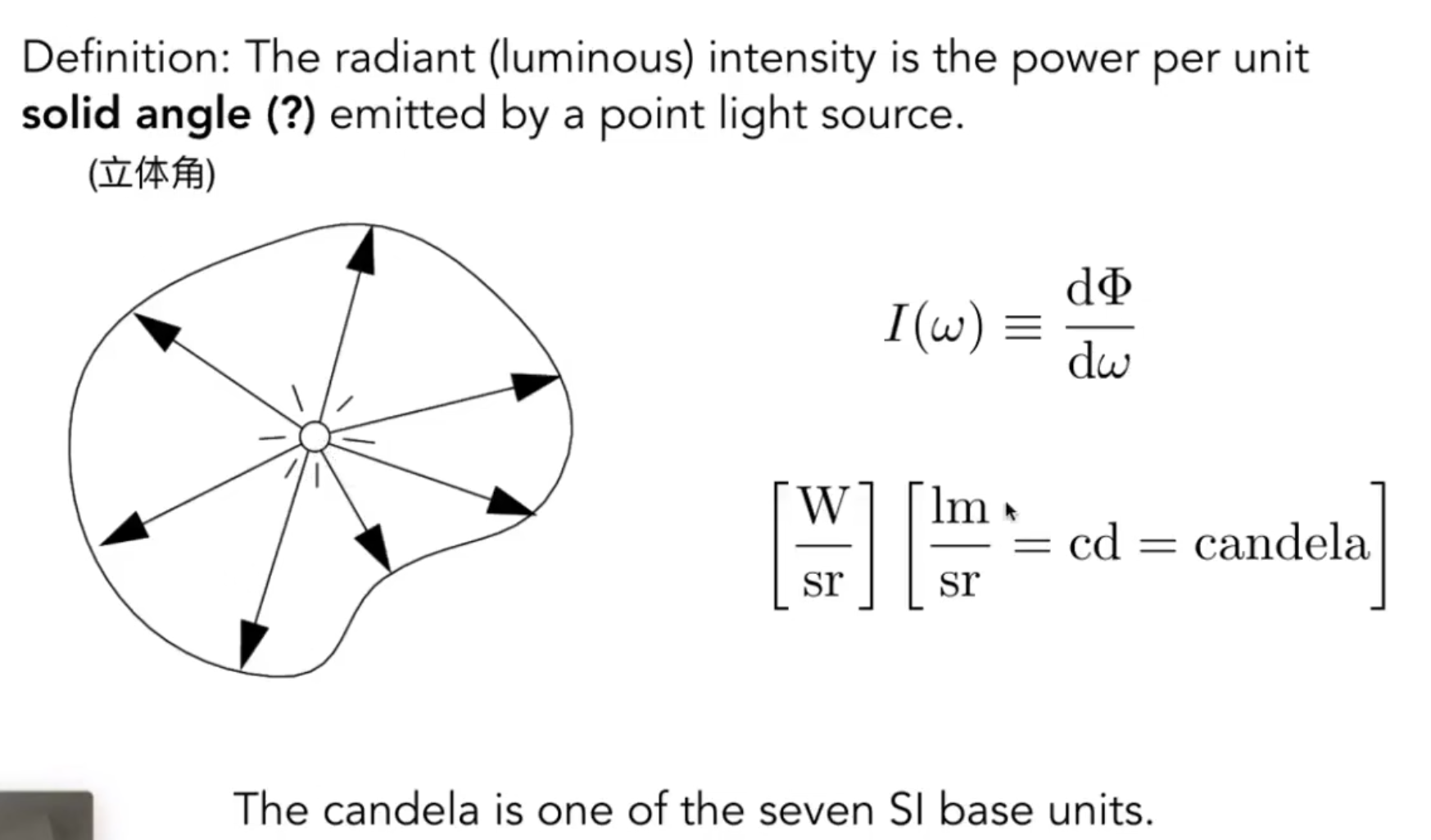
立体角的定义:
弧度制中, 定义弧长和半径的比值是一个角度.

三维中就是面积比上r平方.

我们想求单位立体角. 也就是单位面积下的立体角. 这里就是要求这个小矩形的面积
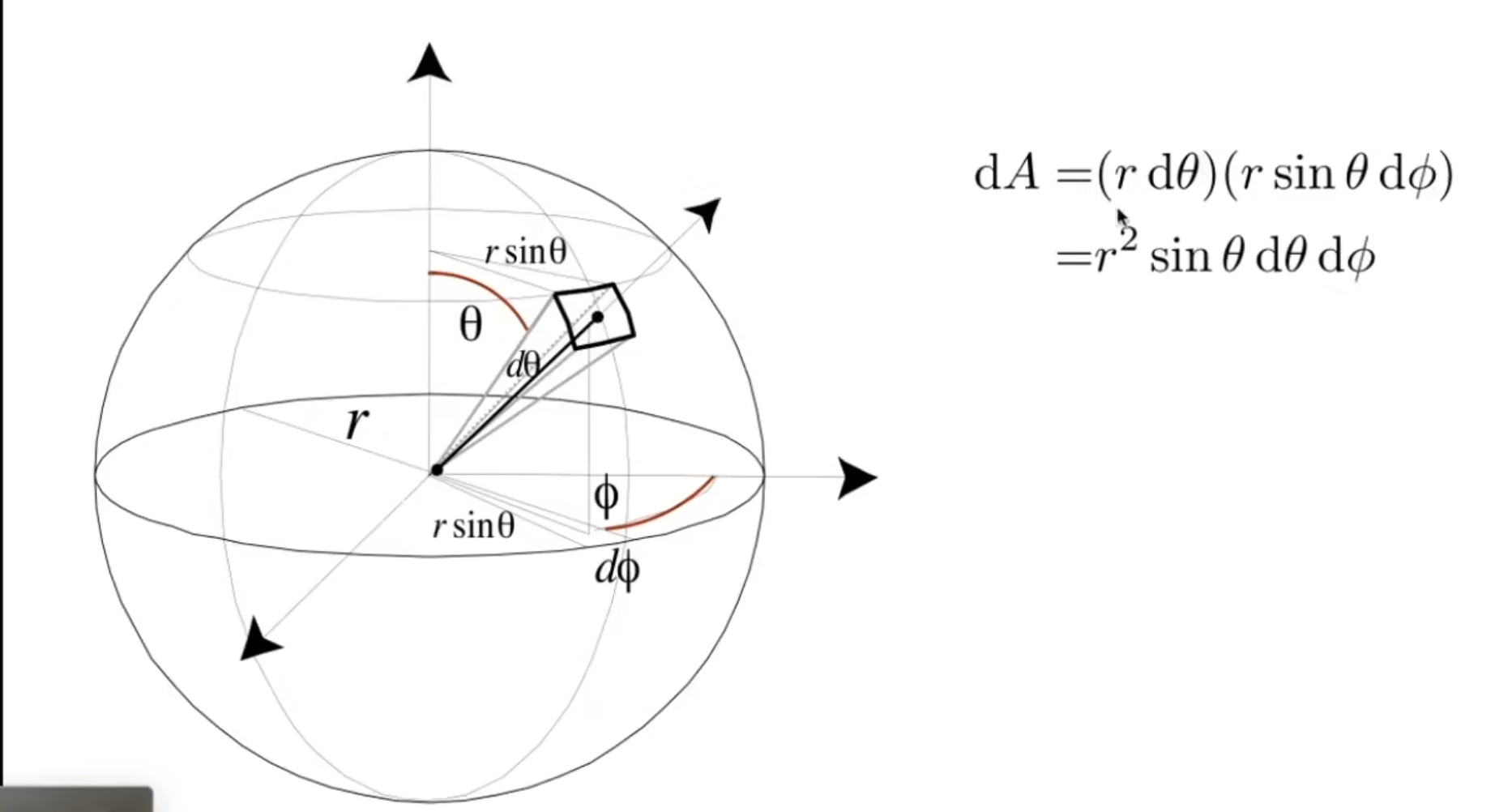
我们将这个矩形分为两个部分: 竖直方向和水平方向. 视竖直方向与z轴的角度为θ, 看作向量沿着竖直圆周移动. 那么由弧度的定义, 就能得到弧长为\(rdθ\). 此时, 水平方向视为在当前高度下沿着水平的圆周移动, 因此有效半径为\(rsinθ\). 因此弧长为\(rsinθΦ\). 所以面积如上公式所示.
那么单位立体角:
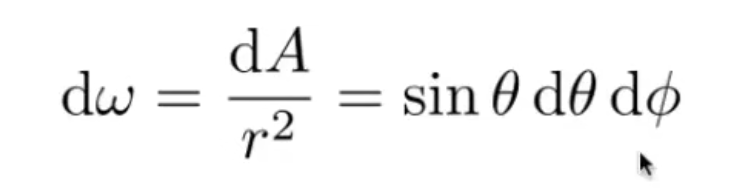
对着\(θ\)求0到\(Π\)的积分, 对着\(Φ\)求0到\(2Π\)的积分, 结果即为整个球的立体角.
回到intensity. 显然:
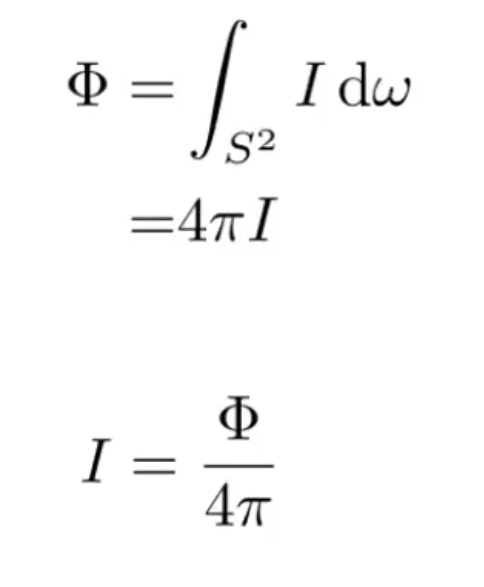
有一个需要强调的理解是: intensity对应的是沿着每个单位立体角的flux大小, 而单位立体角是空间中的"一块"角度, 其对应的是"一捆"光线.. 可以想象一个球体, 然后从圆心延伸出一块四棱锥. 四棱锥顶端的尖尖角就是立体角. 显然, 这个四棱锥可以含有非常多的光线.
--irradiance: 单位面积接收的从各个方向到达的flux. 注意, 这里所说的flux, 是指有效flux. 即垂直于当前表面方向的flux. 所以往往还要乘上一个cos.


从irradiance可以定义先前说的"衰减". 考察一个球, 光源在球心. 则intensity是光源朝某个单位立体角辐射的能量, 随着半径增大, 实际上对应的球面面积和半径都在增大, 最后得到的intensity是不变的. 而对于irradiance. 假设面积不变, 那么随着半径增大, 其对应的立体角在减小. 因此其对应的flux在减小. 所以最后的irradiance减小, 此即衰减.
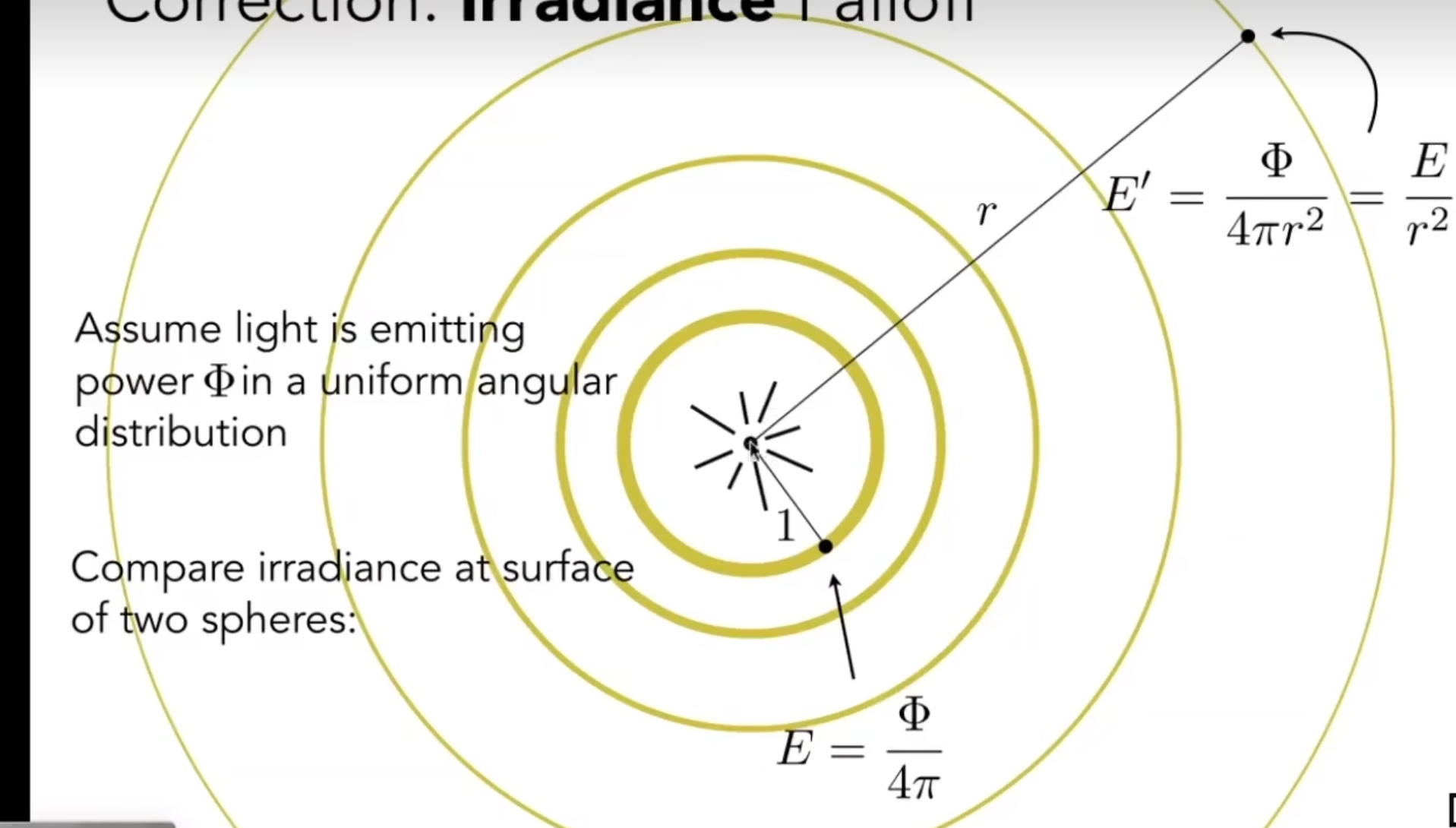
上图中, 单位面积是1, 因此当半径为1的时候E是总的flux除以\(4Π\). 当半径为r的时候, E'是总的flux除以\(4Πr^2\). 衰减系数为\(r^2\).
--radiance: 可以理解为描述一束光线的属性. 这可以与我们先前的intensity概念相联系. intensity是"一捆"光线, 而radiance是一束, 或者说一条光线. 其定义就是: 单位面积单位立体角上的flux大小. 从计算的角度来讲, 可以由intensity对单位面积微分得到; 而另一方面, 也可以从irradiance对单位立体角微分得到. 这里注意, 不论是哪一种方式, 都要注意面积指的是有效面积. 基本上来说都要乘上一个cos.
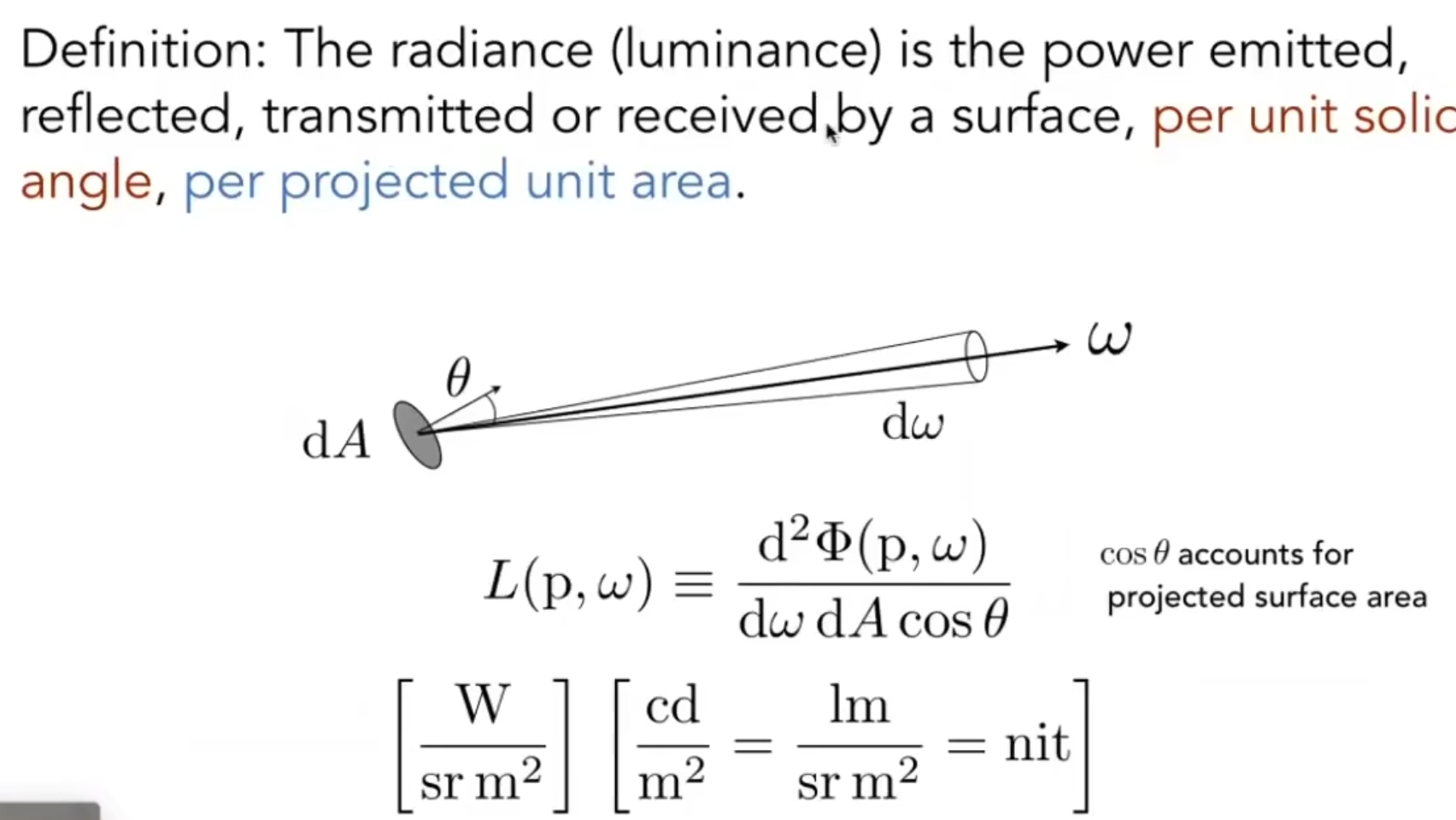
radiance既可以用于接收的flux, 也可以用于辐射的flux. 其本身是对光线的描述, 物理意义取决于光线本身. 式中的Acosθ就是前面提到的有效面积了.
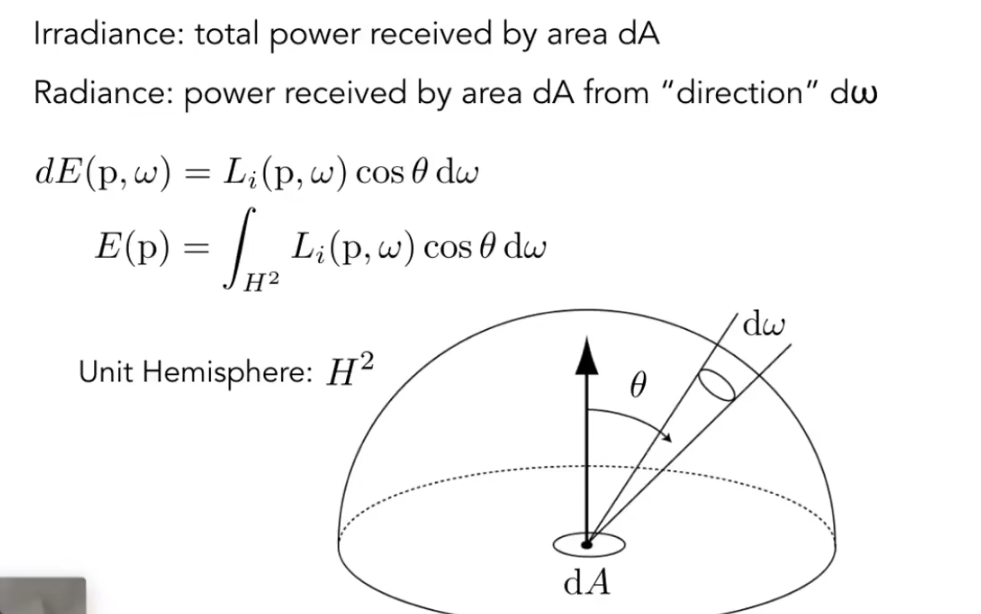
实际上, irradiance就是对当前表面的各个立体角方向的radiance做半球积分:
BRDF
简单来说, 就是一个用来定义材质表面的函数. 它决定了从某个方向入射的光将在吸收后朝哪个方向出射多少光.
比如, 对于一个光滑的表面, 其BRDF可能就是吸收了某个方向的radiance后, 往镜像方向辐射出一束大小几乎相同的radiance. 而对于一个粗糙表面, 其BRDF可能就是吸收了某个方向的radiance后, 朝所有方向均匀辐射出大小相同的radiance.
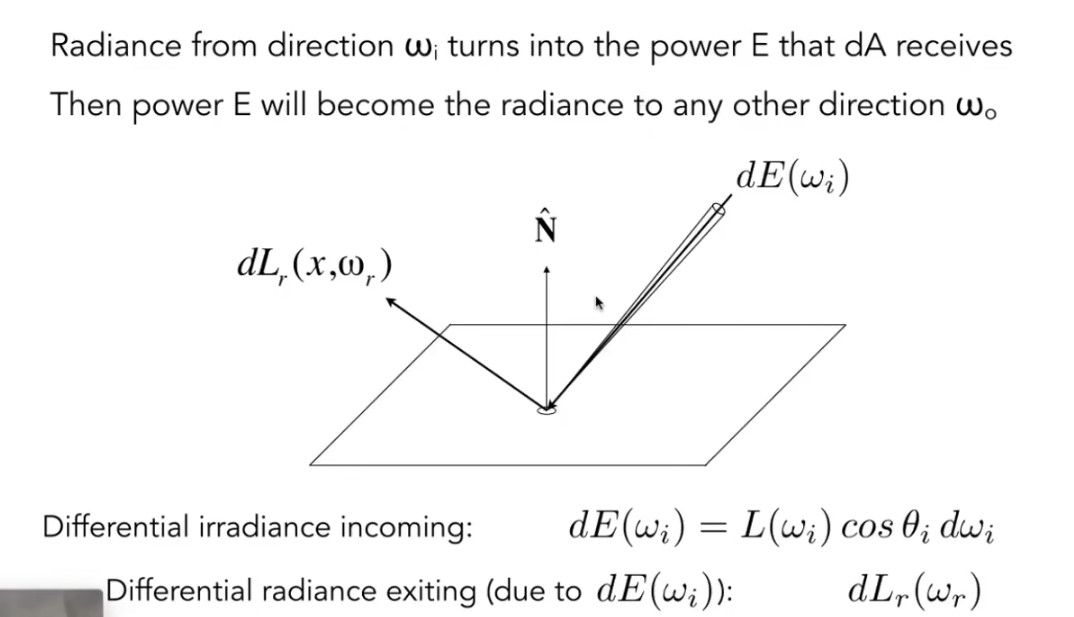
这里, E指的是入射flux. 我们让radiance乘上cos, 使其成为有效的, 然后乘以立体角的微分dw, 显然, 对此式求积分即为当前表面从各个方向接收的flux, 即irradiance. 我们的目的是求出特定方向的radiance. 而BRDF定义的是: 从某个方向射入的radiance, 最终会朝某个方向辐射多少radiance. 显然这是一个比例.
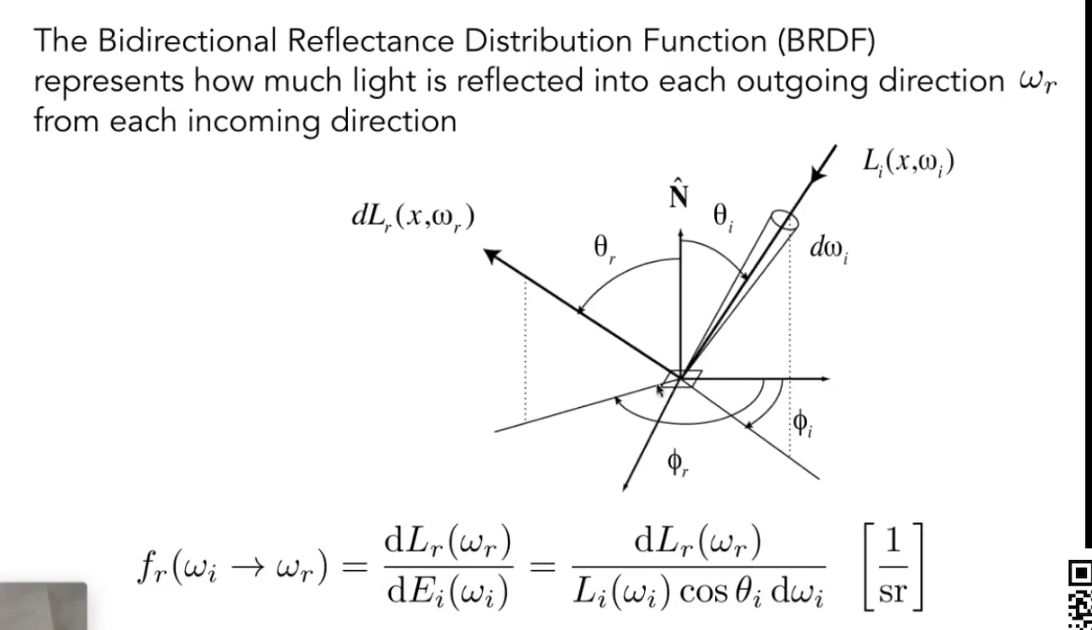
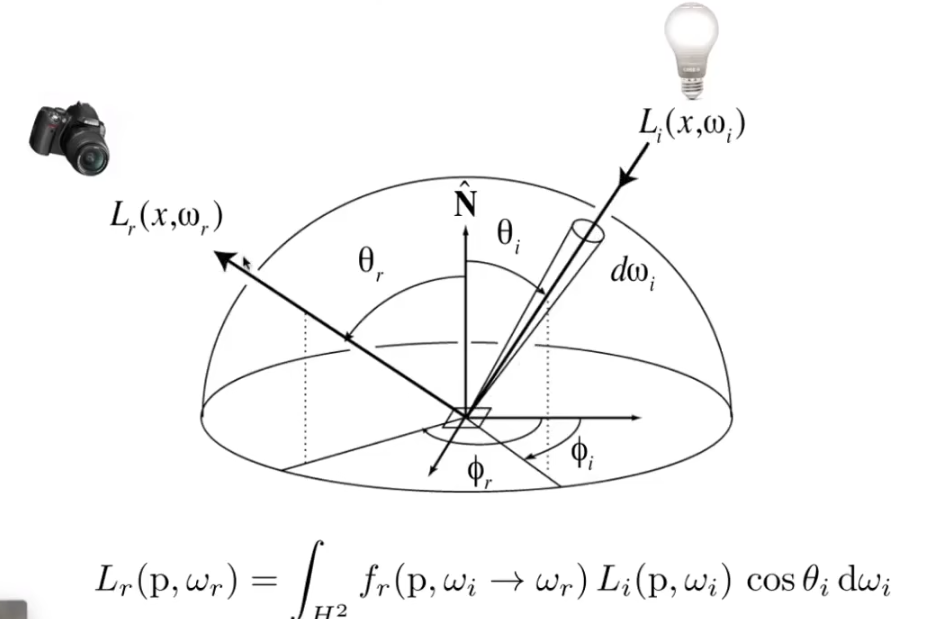
对于所有的入射radiance, 我们都通过当前表面的BRDF计算出每个入射radiance最终会往我们指定的方向辐射多少radiance. 所有入射radiance的贡献加起来就是指定方向的出射radiance了. 由此, 我们实际上就得到了反射方程: 比例 × 入射radiance × cos, 求积分.
而渲染方程, 实际上就是在此基础上加入一个自发光.
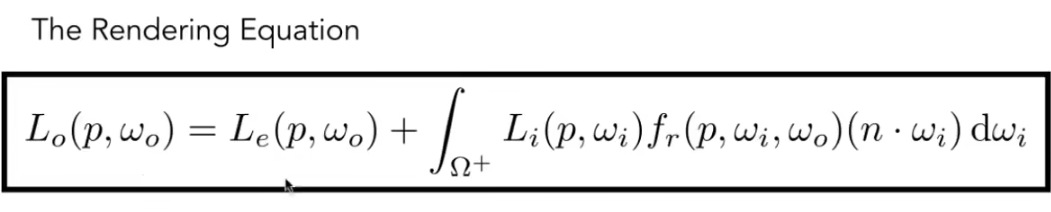
另外, 我们假定所有radiance都朝着表面往外的方向.
对于一个点光源, 我们就能视为其向当前点射出一条radiance. 而对于面光源, 我们视为点光源的集合. 对于从其他表面辐射出来的radiance, 同样视为点光源的集合. 因此, 用后半部分的积分实际上就统一了所有的光照计算.
而对渲染方程一个重要的理解是: 当前点朝指定方向辐射出的radiance, 也会成为其他点的入射radiance. 我们的渲染方程, 最终实质上是一个递推方程.
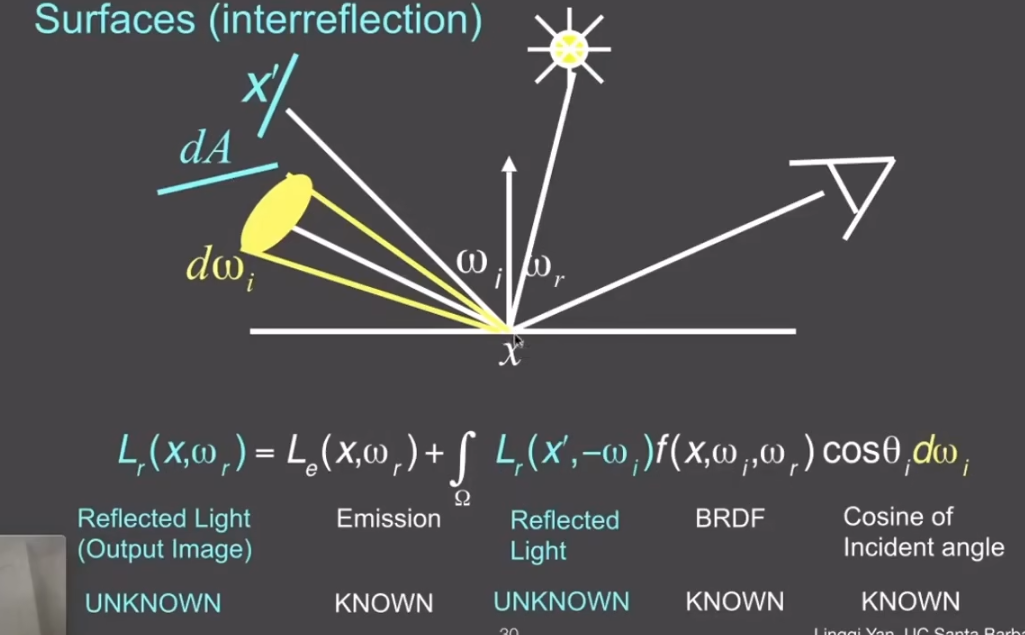
基于这个理解, 我们可以来求解这个递推方程. 由于我没有学过积分算子, 所以这里放一下ai给出的定义.

在视频中, 渲染方程被如下简化, 形似积分算子.

然后继续简化

这里看文字, 要将L和E理解为向量. 抽象地感受一下似乎有点懂了, 不过因为没有学过算子, 还是不可能完全看懂的. 有点将积分转为向量内积的意思. 然后向量维度无限延伸, 同时级数收敛所以两个L是相同的. 我也不知道我在讲什么, 但感觉到了就好, 主要是能够接收这个简化.
这之后就是求解这个矩阵方程的问题了, 涉及一点数值分析.

最后得到的结果, K的次方代表弹射次数,
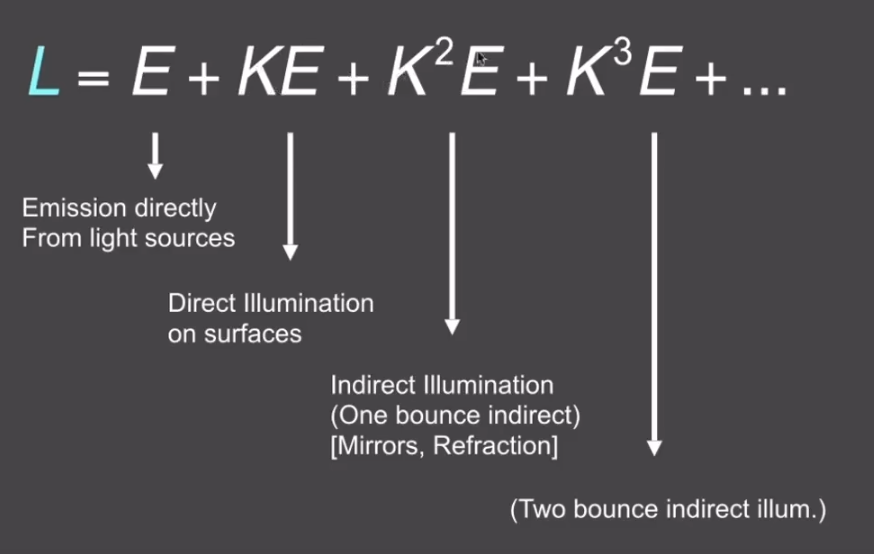
蒙特卡洛路径追踪
概率密度函数 PDF
概率密度函数. 没学过概率论的话(我就是)初次接触很不好理解这个概念.
首先回忆一下高中的概率知识. 随机变量X是啥还记得吗? 比如骰子, 有六个取值可能, 这六个就是随机变量X的取值: 1, 2, 3, 4, 5, 6. 然后每个随机变量会对应一个概率. 显然在这个例子中概率都是1/6. 并且, 在这个例子中, 随机变量X是离散的. 显然, 会有X是连续的情况出现, 比如人群中的身高. (这里的"连续"并不严谨, 意思传达到了就行)
而PDF是这样一个曲线:
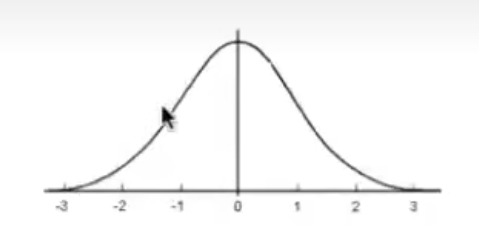
横坐标代表随机变量X, 纵坐标代表概率密度. 一个重要的点是: 曲线围成的面积是1.
这是概率密度函数的特征. 它是用来描述X的分布情况的. 有这个结论:
X取某个区间的时候, 这个区间对应的曲线围成的面积, 就是X取这个区间的概率.
比如上面这个图, X取-1到1的概率是曲线在-1到1之间围成的面积.
这里有一点要强调, 如果问X取某个点的概率, 该怎么算? 实际上, X取某个点的概率是0.
PDF只对区间有效. 这是因为如果X取某个点有概率, 那么在这个点的随便一个邻域可以取无穷多个点, 然后大家都有概率, 最后PDF的面积将会是无穷. 所以, PDF只对区间有效.
另一个理解是, 从纵坐标的意义来看. 概率密度, 描述的是一个密度. 一个没有长度, 没有面积, 没有体积的点, 密度对其也毫无意义.
那连续性的随机变量对应的PDF, 就像上面这个图这样, 如果随机变量离散呢? 比如骰子, 只有六个取值?
那结果就会是柱形图一样的效果:
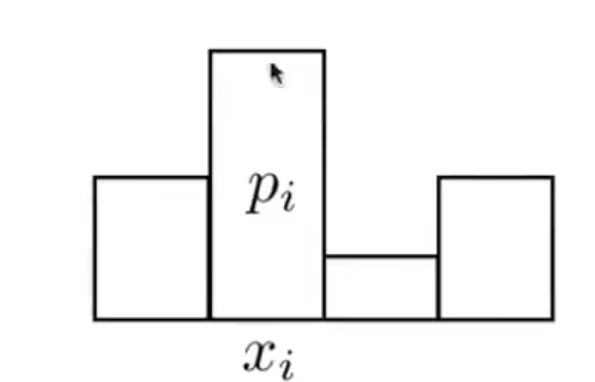
与我们刚才讲的PDF并不矛盾, 柱形图不就是让PDF变成分段函数而已嘛. X取某个离散的值, 可以视为取某个区间.
再强调下, 笔者还没学过概率论, 讲的东西不太严谨, 讲究一个能用就行, 海涵.
希望看到这您能尽量完成对PDF的直观理解.
蒙特卡洛积分
求定积分. 用黎曼积分的方法就是取很多小的长方形, 最后加起来. 用蒙特卡洛的方法就是, 每次取a到b中间的一个值, 得到其函数值, 用这个函数值作为长方形的宽, 用b-a作为长方形的长, 算出长方形的面积. 采样足够多次, 把所有长方形的面积加起来取个平均即为结果.
蒙特卡洛积分常用于求表达式未知或复杂的积分.
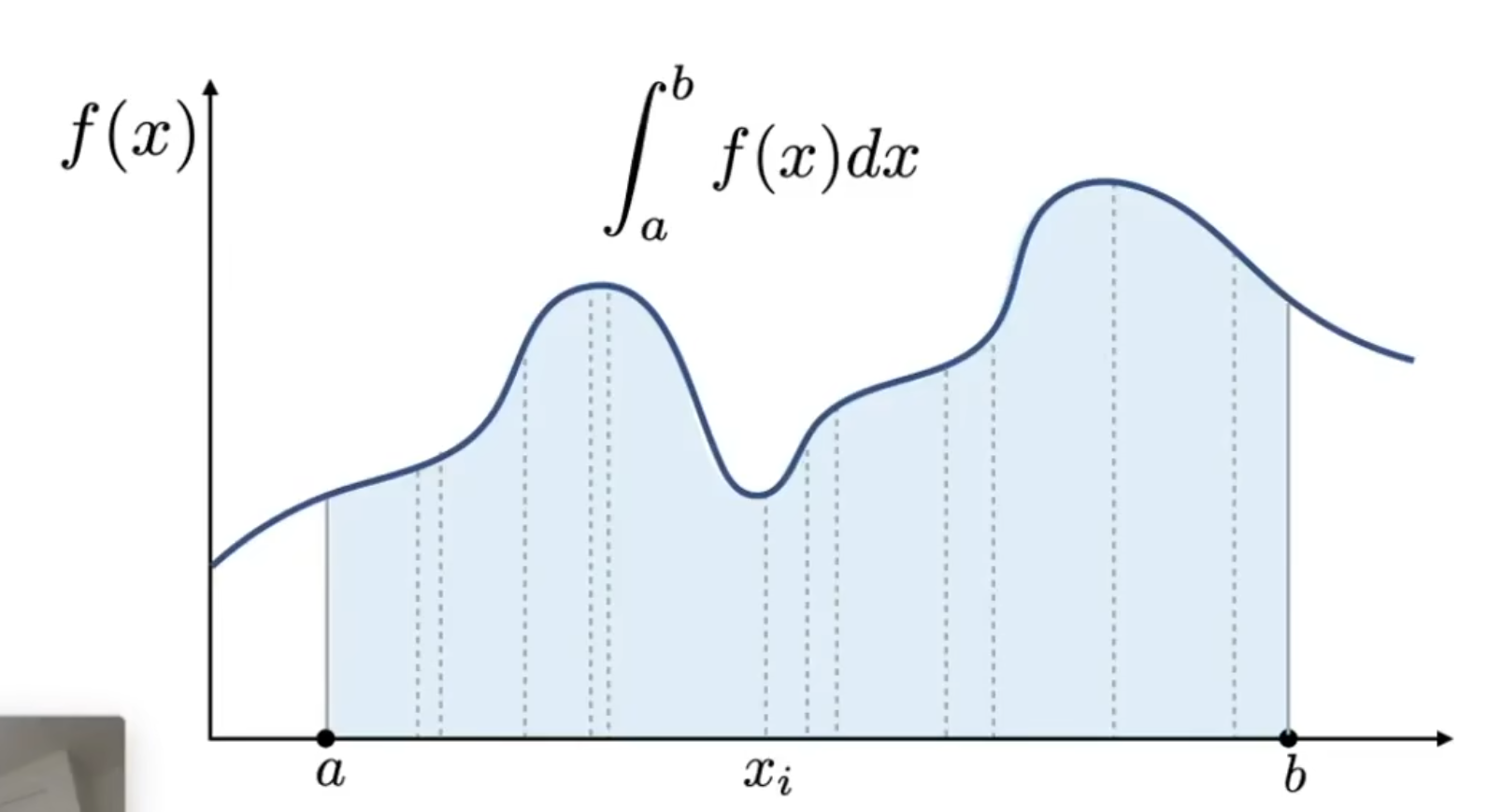
这就遇到第一个问题, 为什么用蒙特卡洛方法, 然后平均起来就是正确结果.
实际上只要取得点足够多. 那么对应的函数值就足够多, 这时候取个平均, 相当于取了函数值的平均值. 所以对应的矩形面积当然就是定积分的值. 就像我们物理中求变力做功, 如果能够得到变力的平均值, 那么用平均乘以路程即可. 难点在于求平均, 而当我们采样点足够多的时候, 得到的平均值就能无限逼近函数整体的平均值.
"平均"这一点理解好以后, 明确一下我们做蒙特卡洛积分的步骤:
--生成随机数
--用这个随机数来采样
--将采样结果求期望(或者说平均)
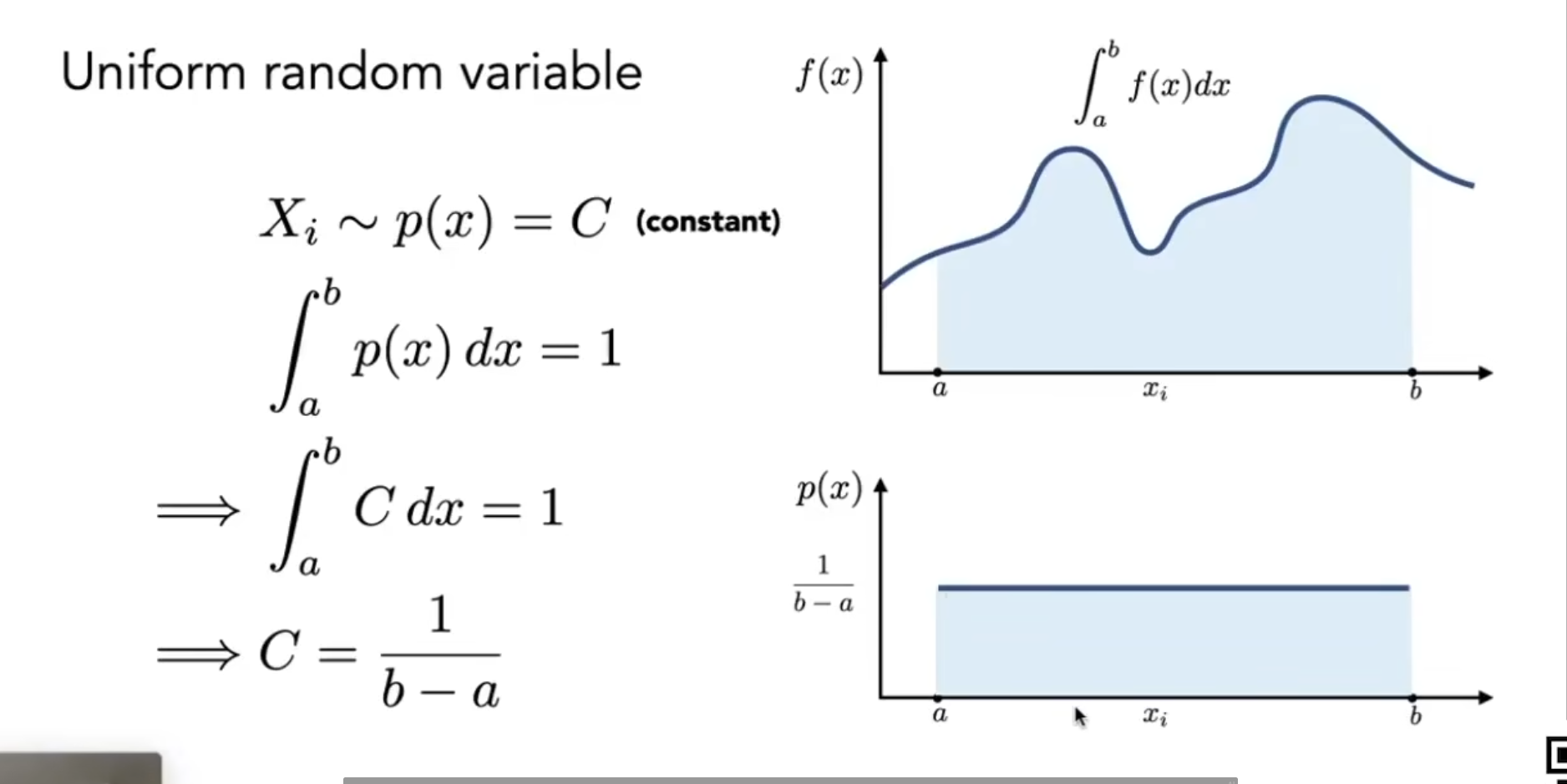
假定我们的x均匀分布, 显然我们只需要采样足够多次, 然后取平均, 最后乘以b-a即可得到面积.
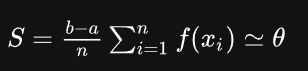
↑很多文章都像上面这样讲, 问题来了, 啥叫x均匀分布? 至少, 我们的目的是对函数求积分, 而似乎从没听说过求积分还分x均不均匀的. 所以我个人认为这个讲法是有点含糊不清的意味的. (当然, 这个式子肯定是对的, 就是正常地在a到b之间采样, 然后算平均值, 算面积.)
什么才是正确的理解呢? 其实, 以上面那个函数图为例, 我们只要在a和b之间取足够多的点, 是不是必定能够得到准确的平均值? 所以问题不在于所谓均不均匀分布, 而在于, 我们不可能取无数个点来得到准确值. 我们的结果是对精确值的估计, 我们要做的, 是最短时间内完成估计的收敛.
所以, 我们知道要采样, 要算平均; 我们希望的是尽可能少地采样, 尽快得到结果.
所以, 我们实际上是生成一系列满足某个分布的随机数, 用这些随机数来采样函数. 前面所谓"x均匀分布", 实际上指的是生成均匀分布的随机数, 然后用这些随机数采样, 而就像前面说的那样, 均匀采样需要非常多的点才能达到比较好的拟合效果. 我们希望有更快的收敛速度, 所以想用少量的随机数达到不错的拟合效果. 显然, 这些随机数需要满足某个特定分布, 显然, 这个分布与我们要求定积分的函数有关.
如何做呢? 首先为x指定一个PDF. 这个PDF描述了x的分布情况. 实际上这样讲依旧含糊不清, 先看式子吧:
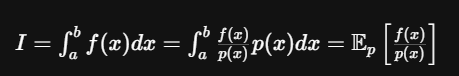
对积分进行恒等变形, 这个p(x)就是我们指定的PDF. 重点看第三个项. 这个式子是最不好理解, 最关键的式子.
我们在干什么? 求期望. 随机采样之后, 求期望. 我们的恒等变形也是往这个方向在靠.
我们现在实际上在做的是: 指定"取这个x的时候, 这个x对应的概率是多少". 回忆一下求期望的公式, 是不是随机变量×概率, 然后求和? 对应我们的这个式子, "概率"部分指的是后半部分p(x)dx.
得益于微分dx的"微小区间"的性质, p(x)dx就是一个概率. 忘了的话可以回看PDF那部分内容.
剩下的就是解决"随机变量"这个部分了. 这部分也是我理解了半天的部分. 同样是其他文章几乎不讲的部分.
很显然, fx/px的大小与px成反比, 从直观上理解, 就是"这个x对应的概率"越低, 其对应的"随机变量"就要大. 当然, 由于fx/px不仅与px有关, 还跟fx有关, 所以应该是: 其对应的"fx"就要被"放大". 这个放大后的整体, 即fx/px, 就是"随机变量".
求期望就求期望, 为啥要放大随机变量呢? 当然可以说变形结果就是这样, 但我就是想直观理解它呢?
现在从整体的情况考虑, 这个问题先留着, 马上就清楚了.
我们为x指定了PDF, 下一步是: 我们按照这个PDF来生成随机数.
那是不是概率大的区间生成的随机数多, 概率小的区间生成的少? 这时候, 用这些数代入上面的式子. 结果就是定积分的估算值了. 而我们前面提到, 想要精确估计定积分, 需要采样足够多的点; 我们在这里生成的随机数并不够多, 并且大部分集中在概率大的区域, 此时fx/px就发挥作用了. 我们虽然只在概率小的区间生成了少量的采样点, 但是他们采样的结果, 我们将其贡献"放大"了. 而对于采样多的区间, 我们将其贡献"缩小"了. 这是一种"抓大放小"的思想, 被称为重要性采样.
有一个结论是: 使用的PDF越贴近fx, 拟合效果就越好. 为啥? 就是因为在fx大的地方, 我们的PDF也大, 那么就有更多的随机数分布在那块区域, 我们能够很快地"接近"fx的定积分的值, 而我们缩小它们的贡献, 能够让整体的值更加精确(每个采样点的权重更小, 对于采样点多的情况, 会获得更精确的结果); 同时对于少量分布在fx小的地方的随机数, 放大它们的贡献, "很快"地"调整"了估算值的大小.
所以这就是我们"放大随机变量"的目的/意义.
所以蒙特卡洛积分的结论:
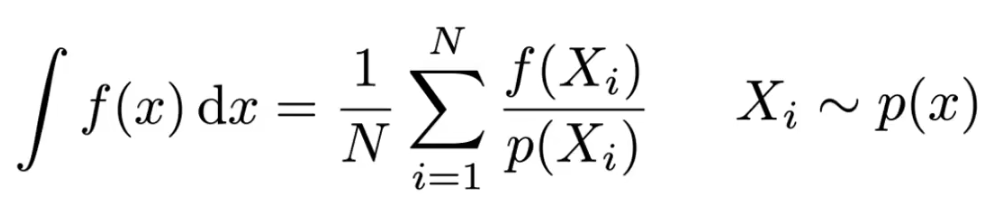
这玩意就是个期望. 对于PDF的选择, 要选尽可能贴合fx的PDF. 而如果选择均匀采样, 所对应的结果也只是"需要更多的采样点才能够达成不错的拟合效果".
用法就是: 根据PDF生成随机数, 然后采样, 求期望, 结束.
很简短的一个结论, 只是一两步的恒等变形, 但确实是非常精妙的方法.
路径追踪
解渲染方程, 怎么解. 一个难点是积分, 积分是连续的; 另一个难点是, 渲染方程是个递归的方程.
计算积分的方法就是蒙特卡洛方法.
对于渲染方程, 我们先忽略其自发光项, 同时仅考虑直接光照. 对于一个面光源照射一个物体的场景.
则我们希望求解的积分, 需要明确PDF, 需要明确f(x). 最简单的就是均匀采样, 我们让PDF为\(1/2Π\), 这个值显然是半球对应的单位立体角. 至于为什么是1/2Π, 是因为我们的随机变量必定是在0到2Π之间, 为了让积分结果为1, 则PDF需要取倒数. 关于这一点的推导:

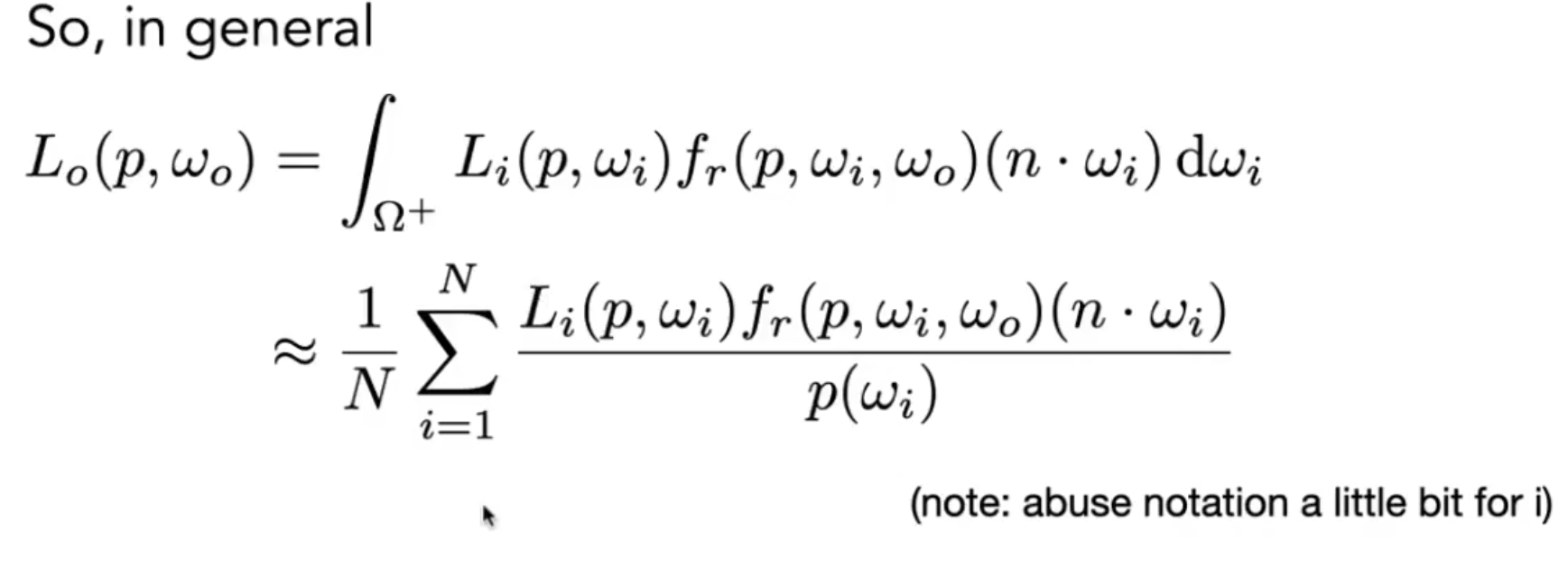

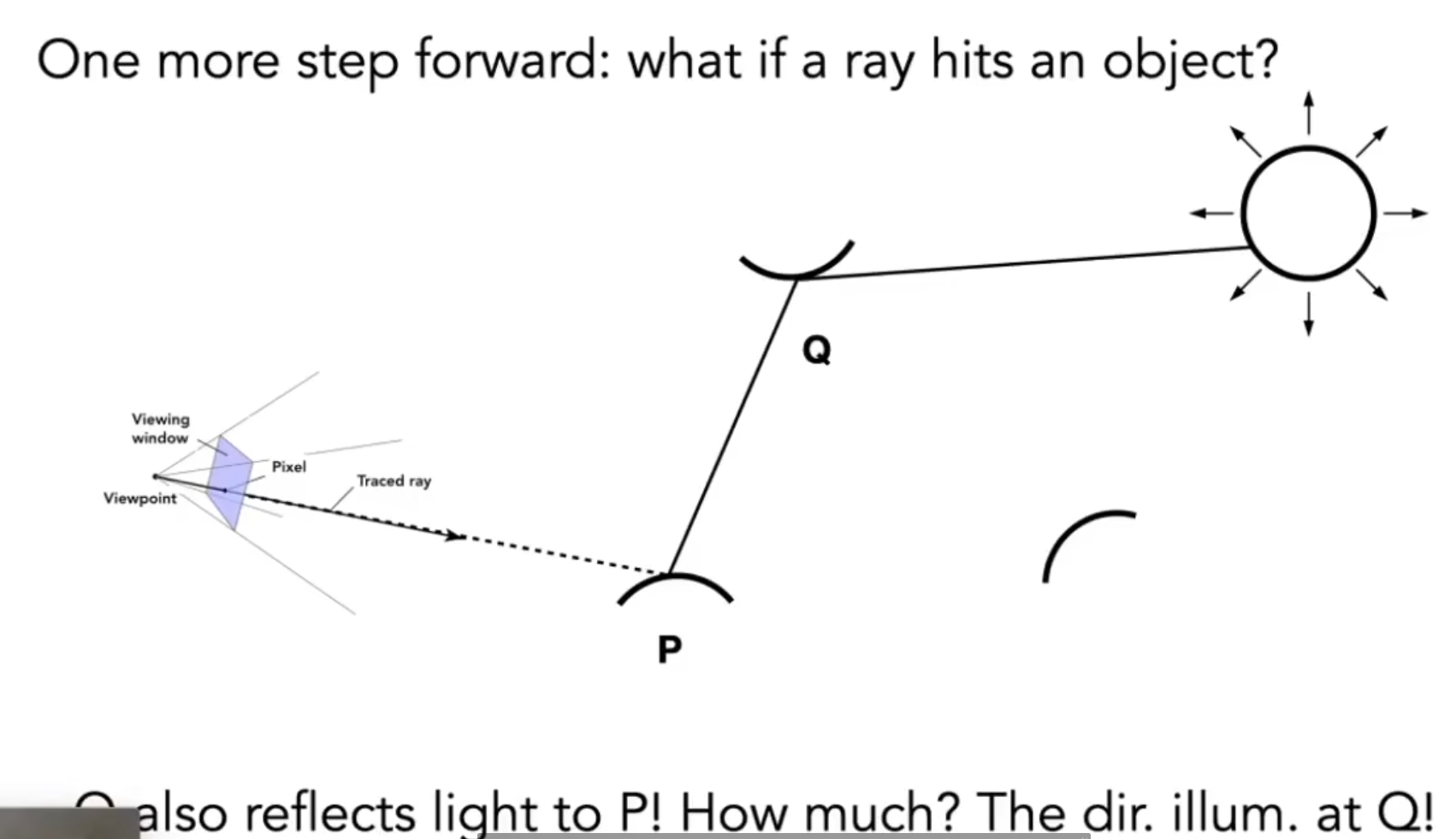
考虑间接光照. 假如打到了另一个物体, 那么相当于从当前点朝该物体看, 计算这条radiance.

光线指数级增长:
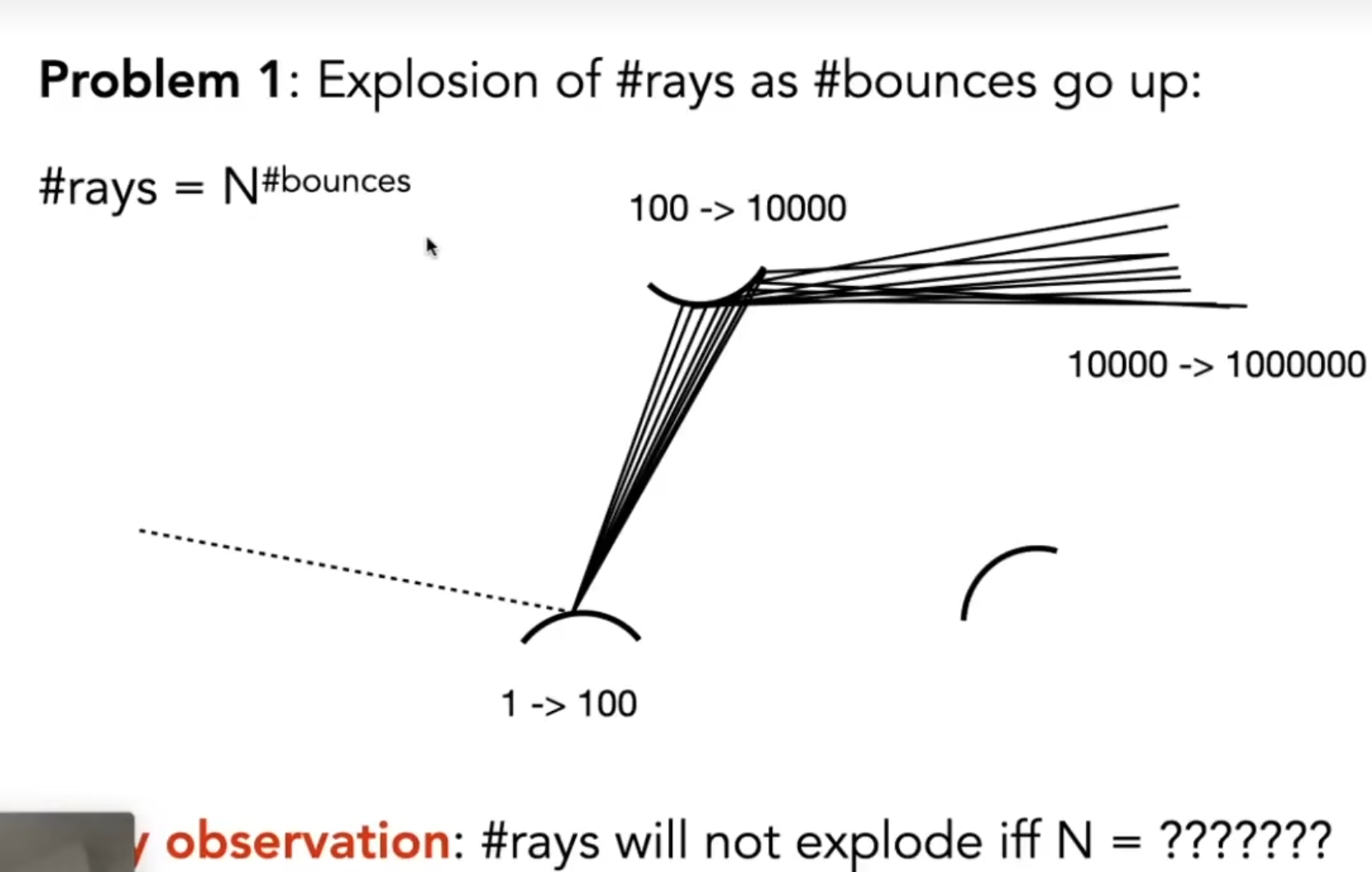
N=1时不会爆炸:

到此, 用N=1来做蒙特卡洛积分, 即为路径追踪. N!=1的时候称为分布式光线追踪.
显然, 只用一根光线会噪声非常大, 不过, 对于一个像素, 我们可以射出多根光线. 这样就人为指定了光线 的数量, 避免指数爆炸.
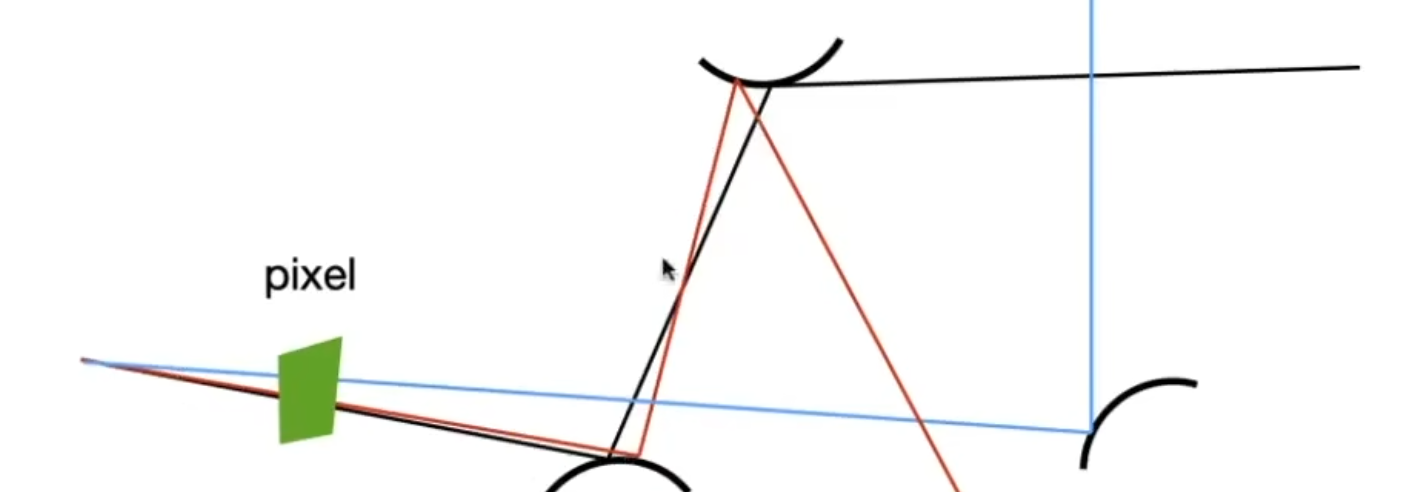

另一个问题, shade这个函数会一直递归, 不会停. 但如果人为设定一个弹射次数限制, 就会导致能量损失.
解决方法是:

我们用RR的方法, 用概率决定是否停止.


至此已经是正确的path tracing方法.

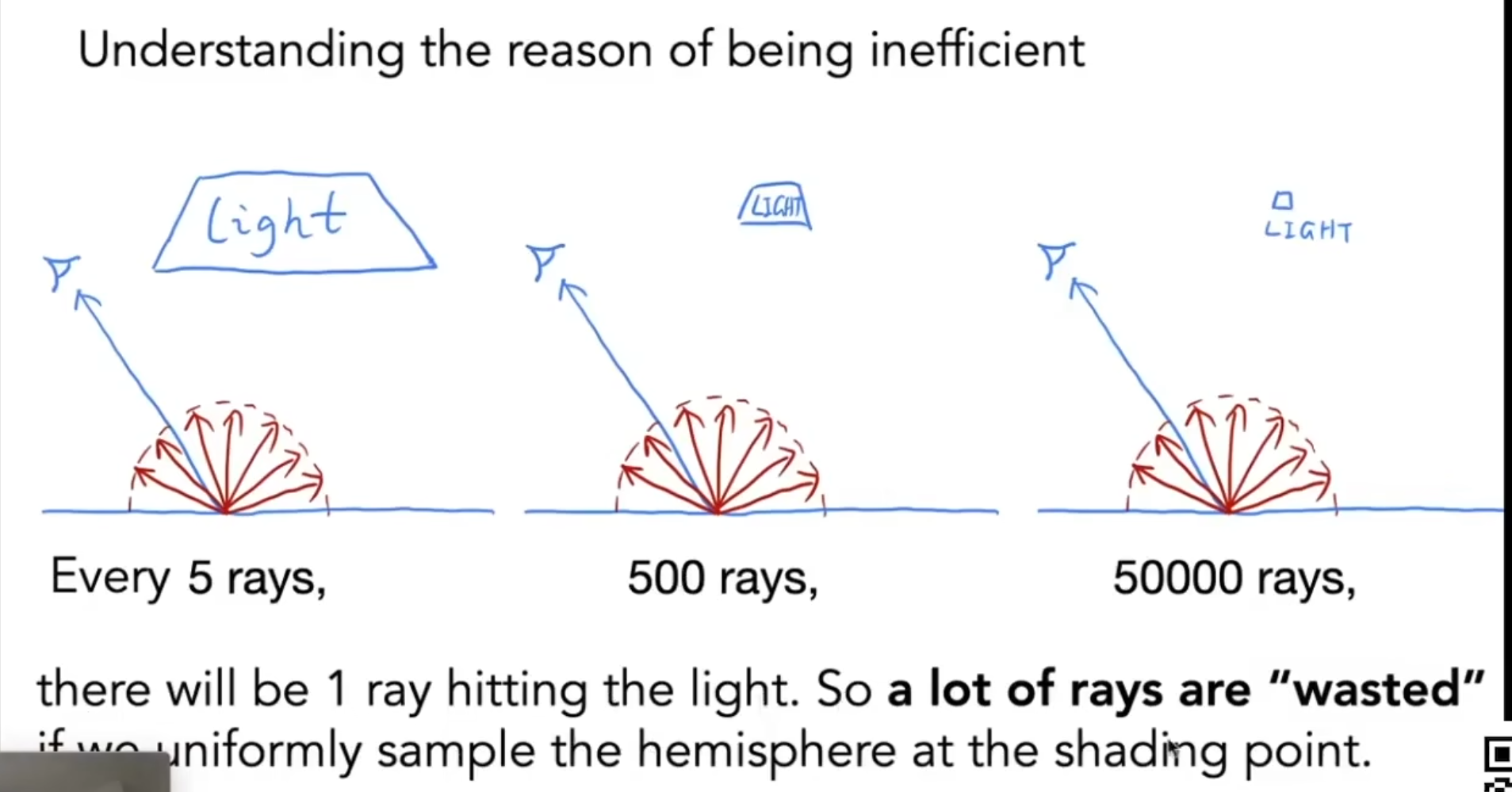

直接在光源上采样. 所以我们必须改成在光源上的积分. 这是因为积分域不同. 对光源采样, 积分域是A, 而对半球采样, 积分域是w. 基于积分换元的想法, 实际上我们只需要找到w和A之间的等式即可. 实际上, 回顾立体角的定义, 是球面上的面积除以半径的平方. 我们只需要让采样面积投影到球面上, 然后除以半径平方即可.
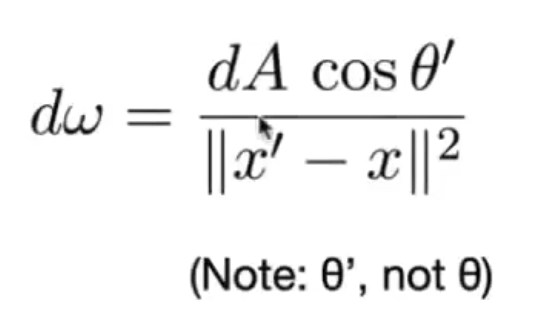
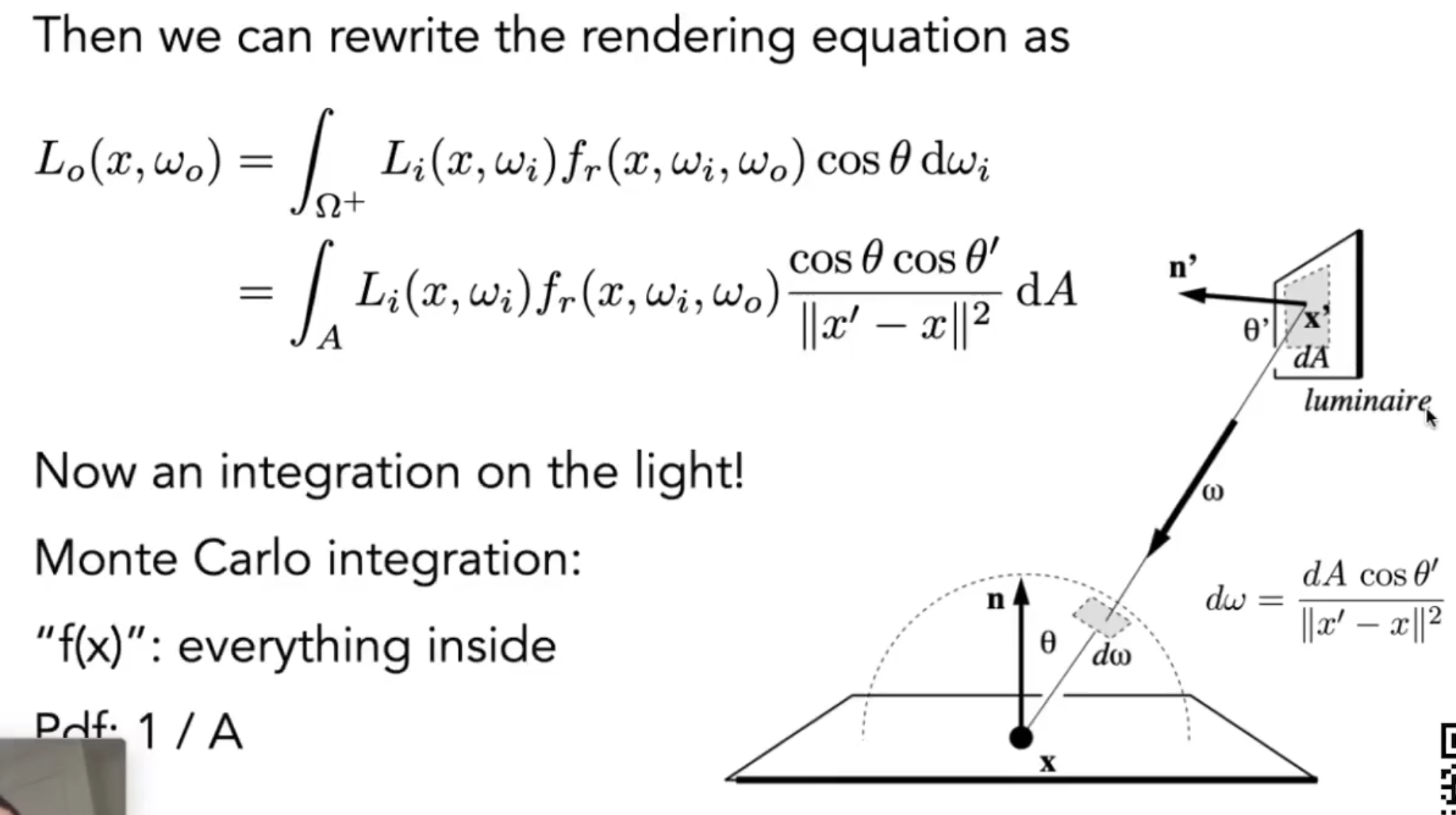


至此剩最后一个小问题...要判断是否被挡到.


一些问题:
--路径追踪不好处理点光源. 如果确实需要, 那将其设置成一个很小的面光源.
--如何均匀采样?(采样理论)
--PDF怎么选更好?(重要性采样)
--能否将光源采样和半球采样结合? 可以. 多重重要性采样
--对像素的着色采样, 最后平均起来是否正确? 还是说要加权?(pixel reconstruction filter)
--最后算出来的radiance不是个颜色, 如何得到颜色?(伽马矫正, 曲线, 颜色空间)
.jpg)